1. Home
  2. Introduction to applied math
  3. Dynamics: force and newton's
  4. Normal, tension, and other

4.6 Normal, tension, and other examples of forces  (Page 7/10)

<< Chapter < Page
  Introduction to applied math     Page 7 / 10
Chapter >> Page >

All the forces discussed in this section are real forces, but there are a number of other real forces, such as lift and thrust, that are not discussed in this section. They are more specialized, and it is not necessary to discuss every type of force. It is natural, however, to ask where the basic simplicity we seek to find in physics is in the long list of forces. Are some more basic than others? Are some different manifestations of the same underlying force? The answer to both questions is yes, as will be seen in the next (extended) section and in the treatment of modern physics later in the text.

Phet explorations: forces in 1 dimension

Explore the forces at work when you try to push a filing cabinet. Create an applied force and see the resulting friction force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

Forces in 1 Dimension

Section summary

  • When objects rest on a surface, the surface applies a force to the object that supports the weight of the object. This supporting force acts perpendicular to and away from the surface. It is called a normal force, N size 12{N} {} .
  • When objects rest on a non-accelerating horizontal surface, the magnitude of the normal force is equal to the weight of the object:

    N = mg size 12{N= ital "mg"} {} .

  • When objects rest on an inclined plane that makes an angle θ size 12{θ} {} with the horizontal surface, the weight of the object can be resolved into components that act perpendicular ( w ⊥ ) and parallel ( w ∥ size 12{w rSub { size 8{ \lline \lline } } } {} ) to the surface of the plane. These components can be calculated using:

    w ∥ = w sin ( θ ) = mg sin ( θ ) size 12{w rSub { size 8{ \lline \lline } } =w"sin" \( θ \) = ital "mg""sin" \( θ \) } {}
    w ⊥ = w cos ( θ ) = mg cos ( θ ) size 12{w rSub { size 8{ ortho } } =w"cos" \( θ \) = ital "mg""cos" \( θ \) } {} .

  • The pulling force that acts along a stretched flexible connector, such as a rope or cable, is called tension, T size 12{T} {} . When a rope supports the weight of an object that is at rest, the tension in the rope is equal to the weight of the object:

    T = mg size 12{T= ital "mg"} {} .

  • In any inertial frame of reference (one that is not accelerated or rotated), Newton’s laws have the simple forms given in this chapter and all forces are real forces having a physical origin.

Conceptual questions

If a leg is suspended by a traction setup as shown in [link] , what is the tension in the rope?

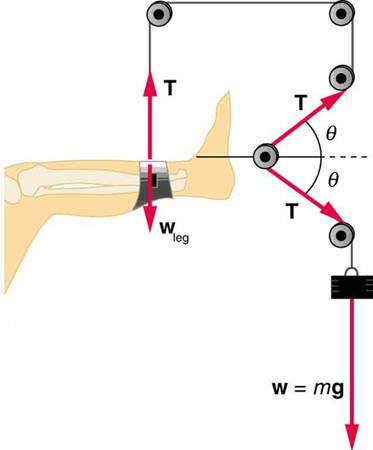
Diagram of a leg in traction.
A leg is suspended by a traction system in which wires are used to transmit forces. Frictionless pulleys change the direction of the force T without changing its magnitude.

In a traction setup for a broken bone, with pulleys and rope available, how might we be able to increase the force along the femur using the same weight? (See [link] .) (Note that the femur is the shin bone shown in this image.)

Problem exercises

Two teams of nine members each engage in a tug of war. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally. (a) What is the acceleration of the two teams? (b) What is the tension in the section of rope between the teams?

  1. 0. 11 m/s 2 size 12{0 "." "11 m/s" rSup { size 8{2} } } {}
  2. 1 . 2 × 10 4 N size 12{1 "." 2 times "10" rSup { size 8{4} } " N"} {}

What force does a trampoline have to apply to a 45.0-kg gymnast to accelerate her straight up at 7 . 50 m/s 2 size 12{7 "." "50 m/s" rSup { size 8{2} } } {} ? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary.

(a) Calculate the tension in a vertical strand of spider web if a spider of mass 8 . 00 × 10 − 5 kg size 12{8 "." "00" times "10" rSup { size 8{ - 5} } " kg"} {} hangs motionless on it. (b) Calculate the tension in a horizontal strand of spider web if the same spider sits motionless in the middle of it much like the tightrope walker in [link] . The strand sags at an angle of 12º size 12{"12"°} {} below the horizontal. Compare this with the tension in the vertical strand (find their ratio).

(a) 7 . 84 × 10 -4 N size 12{7 "." "84" times "10" rSup { size 8{4} } " N"} {}

(b) 1 . 89 × 10 –3 N size 12{1 "." "89" times "10" rSup { size 8{"–3"} } " N"} {} . This is 2.41 times the tension in the vertical strand.

Suppose a 60.0-kg gymnast climbs a rope. (a) What is the tension in the rope if he climbs at a constant speed? (b) What is the tension in the rope if he accelerates upward at a rate of 1 . 50 m/s 2 size 12{1 "." "50 m/s" rSup { size 8{2} } } {} ?

Show that, as stated in the text, a force F ⊥ size 12{F rSub { size 8{ ortho } } } {} exerted on a flexible medium at its center and perpendicular to its length (such as on the tightrope wire in [link] ) gives rise to a tension of magnitude T = F ⊥ 2 sin ( θ ) size 12{T= { {F rSub { size 8{ ortho } } } over {2"sin" \( θ \) } } } {} .

Newton’s second law applied in vertical direction gives

F y = F − 2 T sin θ = 0 size 12{F rSub { size 8{y} } =F - 2T" sin "θ=0} {}
F = 2 T sin θ size 12{F rSub { size 8{ ortho } } =2"T sin "θ} {}
T = F 2 sin θ size 12{T= { {F rSub { size 8{ ortho } } } over {"2 sin "θ} } } {} .

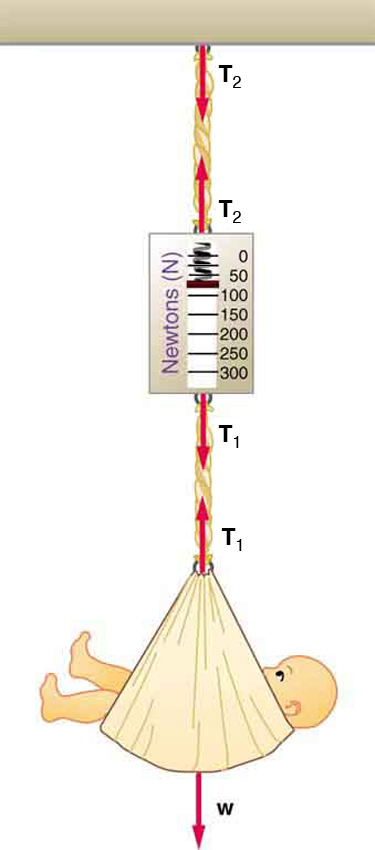
Consider the baby being weighed in [link] . (a) What is the mass of the child and basket if a scale reading of 55 N is observed? (b) What is the tension T 1 size 12{T rSub { size 8{1} } } {} in the cord attaching the baby to the scale? (c) What is the tension T 2 size 12{T rSub { size 8{2} } } {} in the cord attaching the scale to the ceiling, if the scale has a mass of 0.500 kg? (d) Draw a sketch of the situation indicating the system of interest used to solve each part. The masses of the cords are negligible.

A vertical spring scale measuring the weight of a baby is shown. The scale is hung from the ceiling by a cord. The weight W of the baby is shown by a vector arrow acting downward and tension T sub one acting in the cord is shown by an arrow upward. The tension in the cord T sub two attached to the ceiling is represented by an arrow upward from the spring scale and downward from the ceiling.
A baby is weighed using a spring scale.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Introduction to applied math and physics. OpenStax CNX. Oct 04, 2012 Download for free at http://cnx.org/content/col11426/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?

Ask