4.6 Non-ideal gas models  (Page 12/5)

Thus far, the ideal gas law, PV = nRT , has been applied to a variety of different types of problems, ranging from reaction stoichiometry and empirical and molecular formula problems to determining the density and molar mass of a gas. As mentioned in the previous modules of this chapter, however, the behavior of a gas is often non-ideal, meaning that the observed relationships between its pressure, volume, and temperature are not accurately described by the gas laws. In this section, the reasons for these deviations from ideal gas behavior are considered.

One way in which the accuracy of PV = nRT can be judged is by comparing the actual volume of 1 mole of gas (its molar volume, V _m ) to the molar volume of an ideal gas at the same temperature and pressure. This ratio is called the compressibility factor (Z)    with:

Ideal gas behavior is therefore indicated when this ratio is equal to 1, and any deviation from 1 is an indication of non-ideal behavior. [link] shows plots of Z over a large pressure range for several common gases.

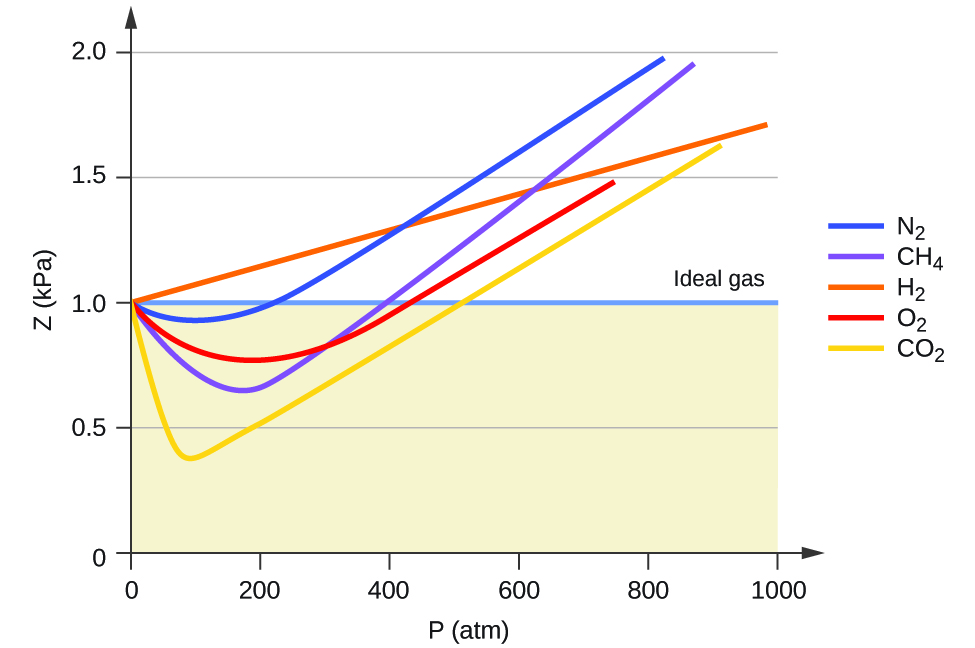
As is apparent from [link] , the ideal gas law does not describe gas behavior well at relatively high pressures. To determine why this is, consider the differences between real gas properties and what is expected of a hypothetical ideal gas.

Particles of a hypothetical ideal gas have no significant volume and do not attract or repel each other. In general, real gases approximate this behavior at relatively low pressures and high temperatures. However, at high pressures, the molecules of a gas are crowded closer together, and the amount of empty space between the molecules is reduced. At these higher pressures, the volume of the gas molecules themselves becomes appreciable relative to the total volume occupied by the gas ( [link] ). The gas therefore becomes less compressible at these high pressures, and although its volume continues to decrease with increasing pressure, this decrease is not proportional as predicted by Boyle’s law.

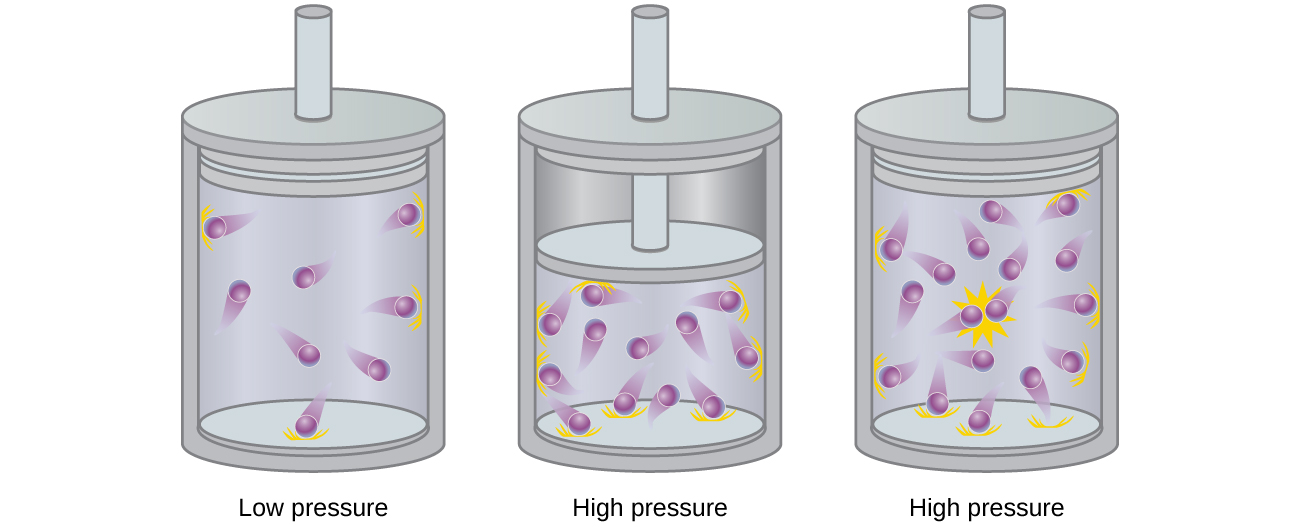
At relatively low pressures, gas molecules have practically no attraction for one another because they are (on average) so far apart, and they behave almost like particles of an ideal gas. At higher pressures, however, the force of attraction is also no longer insignificant. This force pulls the molecules a little closer together, slightly decreasing the pressure (if the volume is constant) or decreasing the volume (at constant pressure) ( [link] ). This change is more pronounced at low temperatures because the molecules have lower KE relative to the attractive forces, and so they are less effective in overcoming these attractions after colliding with one another.