| << Chapter < Page | Chapter >> Page > |
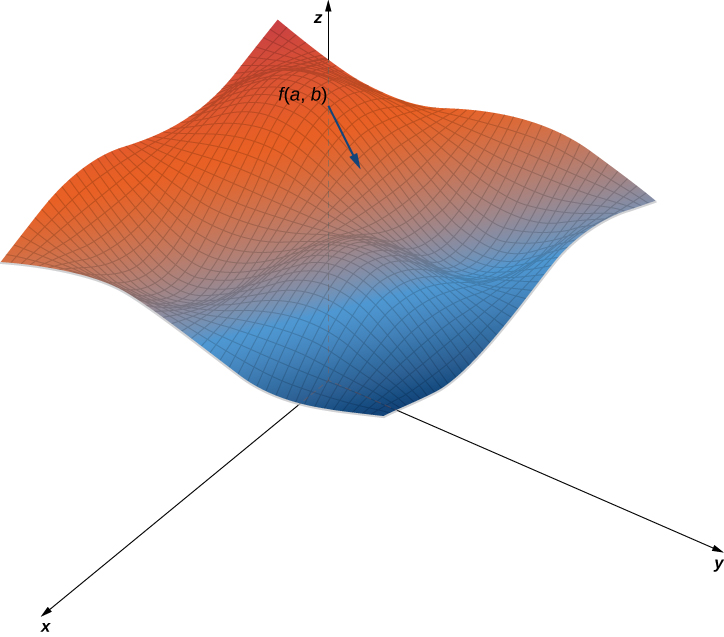
[link] shows a portion of the graph of the function Given a point in the domain of the maximum value of the gradient at that point is given by This would equal the rate of greatest ascent if the surface represented a topographical map. If we went in the opposite direction, it would be the rate of greatest descent.
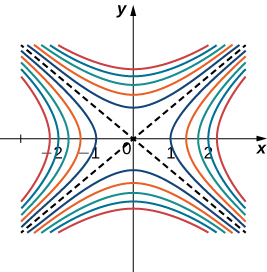
When using a topographical map, the steepest slope is always in the direction where the contour lines are closest together (see [link] ). This is analogous to the contour map of a function, assuming the level curves are obtained for equally spaced values throughout the range of that function.
Recall that if a curve is defined parametrically by the function pair then the vector is tangent to the curve for every value of in the domain. Now let’s assume is a differentiable function of and is in its domain. Let’s suppose further that and for some value of and consider the level curve Define and calculate on the level curve. By the chain Rule,
But because for all Therefore, on the one hand,
on the other hand,
Therefore,
Thus, the dot product of these vectors is equal to zero, which implies they are orthogonal. However, the second vector is tangent to the level curve, which implies the gradient must be normal to the level curve, which gives rise to the following theorem.
Suppose the function has continuous first-order partial derivatives in an open disk centered at a point If then is normal to the level curve of at
We can use this theorem to find tangent and normal vectors to level curves of a function.
For the function find a tangent vector to the level curve at point Graph the level curve corresponding to and draw in and a tangent vector.
First, we must calculate
Next, we evaluate at
This vector is orthogonal to the curve at point We can obtain a tangent vector by reversing the components and multiplying either one by Thus, for example, is a tangent vector (see the following graph).
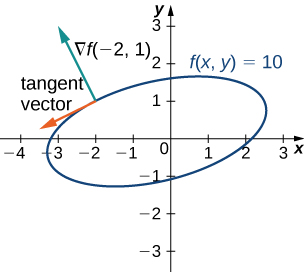
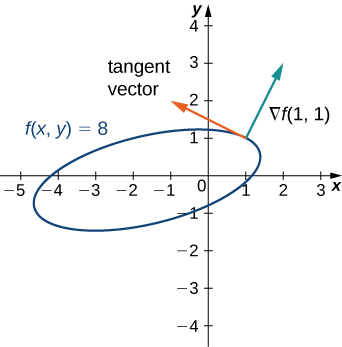
For the function find the tangent to the level curve at point Draw the graph of the level curve corresponding to and draw and a tangent vector.
Tangent vector:
or

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?