| << Chapter < Page | Chapter >> Page > |
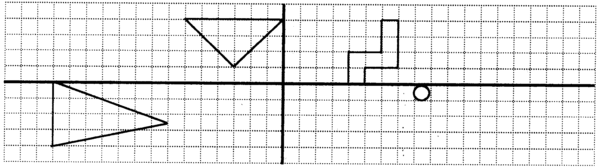
First plot the following points on the given Cartesian plane, connect them in order with straight lines to draw the shape, and then map the coordinates as given to transform the figures.
A(2 ; 2) , B(2 ; 4) , C(4 ; 4) , D(4 ; 6) , E(6 ; 6) , D(6 ; 2) , A(2 ; 2)
A(2 ; 2)→A(12 ; 2) ,
B(2 ; 4)→B(12 ; 4) ,
C(4 ; 4)→C(10 ; 4) ,
D(4 ; 6)→D(10 ; 6) ,
E(6 ; 6)→E(8 ; 6) ,
D(6 ; 2)→D(8 ; 2).
Can you see that the shape is reflected in the line on the grid? This means that if you were to fold the grid on the line, then the shape will fall on (coincide with) its reflection. In other words, the line of reflection is a line of symmetry for the shape and its reflection. We can also say we are flipping the shape, but this doesn’t tell us where it ends up.

We could say: “Flip the shape to the right and then move it two units to the right.”
Choose one of the shapes above and connect each point of the shape with its corresponding reflected point. Now take the centres of these lines and draw a line through the centres. This is the line of reflection.
On the grid below, draw the position of each shape once it has been reflected in the given line. Note that the line of reflection can go through the figure; it can touch the figure, or be outside it.

We often reflect figures in the x –axis or the y –axis.
You may colour the design in.
ACTIVITY 3
To learn how to transform by rotation, and put translations together
[LO 3.2, 3.7]
Rotation
In the diagram below, there is a point marked X on each shape. Imagine that the shaded shape was cut out and loose. A pin was stuck into the point X, and the shape was turned around the pin so that it fell over the unshaded shape. To specify how far we have to turn it, we have to use angles . For example, the triangle was turned ( rotated ) clockwise through 90°.
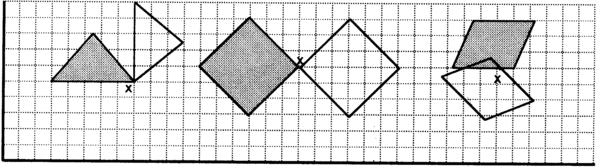
Below you have been given figure A. Draw figure B by reflecting figure A in the given line. Draw figure C by translating figure B 8 units right and 2 units down. Then rotate figure C 180 ° around the point marked X in figure A to give figure D. We can say that figure D is a complex transformation of figure A, as we needed several steps to draw it.

ACTIVITY 4
To enjoy transformations in the form of tilings and tessellations
[LO 3.2, 3.7]
The most remarkable and widely spread use of tessellations can be found in the decoration applied to buildings in the Islamic world. Islam forbids the making of images, so the builders concentrated on shapes. The Persians were competent mathematicians, and this helped to establish the rules of tessellation they used to such brilliant effect in the mosques and other important cultural centres. Even more interesting is the fact that the surfaces were often curved, not flat, which makes the principles of tessellation even trickier.
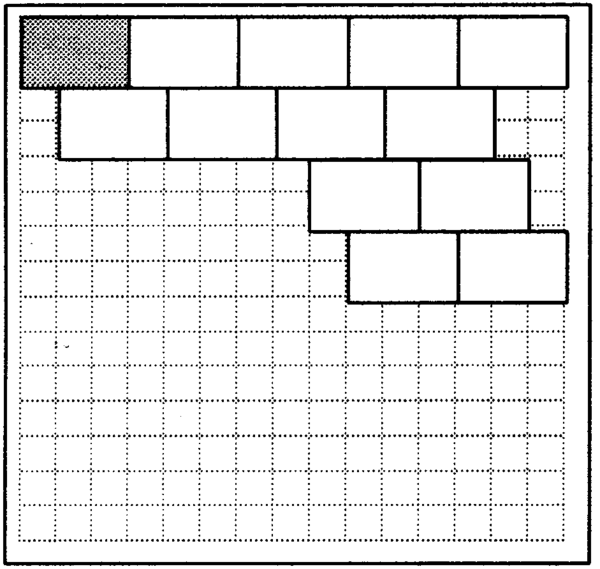
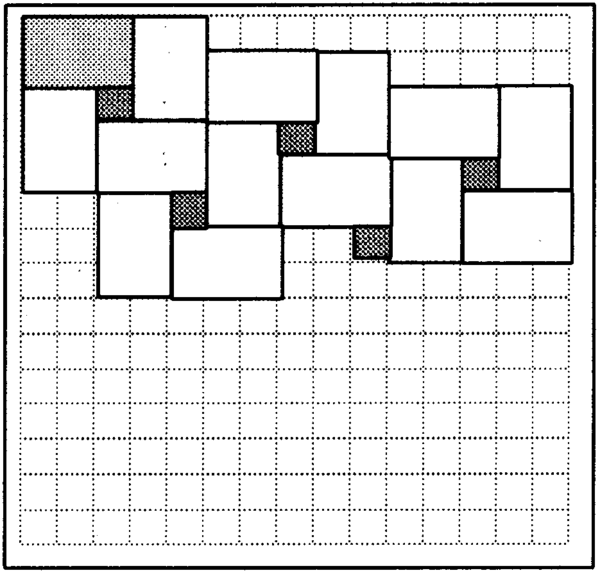


| LO 3 |
| Space and Shape (Geometry)The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three–dimensional objects in a variety of orientations and positions. |
| We know this when the learner: |
| 3.2 in contexts that include those that may be used to build awareness of social, cultural and environmental issues, describes the interrelationships of the properties of geometric figures and solids with justification, including: |
| 3.2.2 transformations. |
| 3.3 uses geometry of straight lines and triangles to solve problems and to justify relationships in geometric figures; |
| 3.4 draws and/or constructs geometric figures and makes models of solids in order to investigate and compare their properties and model situations in the environment; |
| 3.6 recognises and describes geometric solids in terms of perspective, including simple perspective drawing; |
| 3.7 uses various representational systems to describe position and movement between positions, including:ordered grids |

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?