4.4 Exponential functions  (Page 70/2)

Functions of the form $y=a{b}^{\left(x\right)}+q$

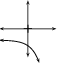
Functions of the form $y=a{b}^{\left(x\right)}+q$ are known as exponential functions. The general shape of a graph of a function of this form is shown in [link] .

Investigation : functions of the form $y=a{b}^{\left(x\right)}+q$

1. On the same set of axes, plot the following graphs:
   1. $a\left(x\right)=-2·b^{\left(x\right)}+1$
   2. $b\left(x\right)=-1·b^{\left(x\right)}+1$
   3. $c\left(x\right)=-0·b^{\left(x\right)}+1$
   4. $d\left(x\right)=-1·b^{\left(x\right)}+1$
   5. $e\left(x\right)=-2·b^{\left(x\right)}+1$
   Use your results to deduce the effect of $a$ .
2. On the same set of axes, plot the following graphs:
   1. $f\left(x\right)=1·b^{\left(x\right)}-2$
   2. $g\left(x\right)=1·b^{\left(x\right)}-1$
   3. $h\left(x\right)=1·b^{\left(x\right)}+0$
   4. $j\left(x\right)=1·b^{\left(x\right)}+1$
   5. $k\left(x\right)=1·b^{\left(x\right)}+2$
   Use your results to deduce the effect of $q$ .

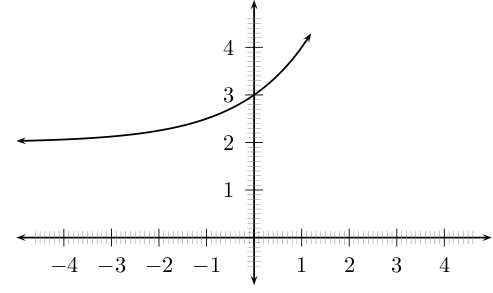
You should have found that the value of $a$ affects whether the graph curves upwards ( $a>0$ ) or curves downwards ( $a<0$ ).

You should have also found that the value of $q$ affects the position of the $y$ -intercept.

These different properties are summarised in [link] .

	$a>0$	$a<0$
$q>0$
$q<0$

Domain and range

For $y=a{b}^{\left(x\right)}+q$ , the function is defined for all real values of $x$ . Therefore, the domain is $\{x:x\in \mathbb{R}\}$ .

The range of $y=a{b}^{\left(x\right)}+q$ is dependent on the sign of $a$ .

If $a>0$ then:

Therefore, if $a>0$ , then the range is $\left\{f\right(x):f(x)\in [q;\infty \left)\right\}$ .

If $a<0$ then:

Therefore, if $a<0$ , then the range is $\left\{f\right(x):f(x)\in (-\infty ;q\left]\right\}$ .

For example, the domain of $g\left(x\right)=3·2^x+2$ is $\{x:x\in \mathbb{R}\}$ . For the range,

Therefore the range is $\left\{g\right(x):g(x)\in [2;\infty \left)\right\}$ .

Intercepts

For functions of the form, $y=a{b}^{\left(x\right)}+q$ , the intercepts with the $x$ and $y$ axis is calculated by setting $x=0$ for the $y$ -intercept and by setting $y=0$ for the $x$ -intercept.

The $y$ -intercept is calculated as follows:

For example, the $y$ -intercept of $g\left(x\right)=3·2^x+2$ is given by setting $x=0$ to get:

The $x$ -intercepts are calculated by setting $y=0$ as follows:

Which only has a real solution if either $a<0$ or $q<0$ . Otherwise, the graph of the function of form $y=a{b}^{\left(x\right)}+q$ does not have any $x$ -intercepts.

For example, the $x$ -intercept of $g\left(x\right)=3·2^x+2$ is given by setting $y=0$ to get:

which has no real solution. Therefore, the graph of $g\left(x\right)=3·2^x+2$ does not have any $x$ -intercepts.

Asymptotes

There is one asymptote for functions of the form $y=a{b}^{\left(x\right)}+q$ . The asymptote can be determined by examining the range.

We saw that the function was undefined at $y=q$ . Therefore the asymptote is $y=q$ .

For example, the domain of $g\left(x\right)=3·2^x+2$ is $\{x:x\in \mathbb{R}\}$ because $g\left(x\right)$ is defined for all $x$ . We also see that $g\left(x\right)$ is undefined at $y=2$ . Therefore the range is $\left\{g\right(x):g(x)\in (-\infty ;2)\cup (2;\infty \left)\right\}$ .

From this we deduce that the asymptote is at $y=2$ .

Sketching graphs of the form $f\left(x\right)=a{b}^{\left(x\right)}+q$

In order to sketch graphs of functions of the form, $f\left(x\right)=a{b}^{\left(x\right)}+q$ , we need to calculate determine four characteristics:

1. domain and range
2. $y$ -intercept
3. $x$ -intercept

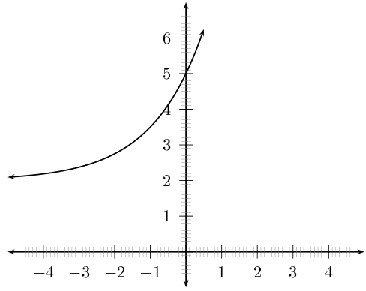
For example, sketch the graph of $g\left(x\right)=3·2^x+2$ . Mark the intercepts.

We have determined the domain to be $\{x:x\in \mathbb{R}\}$ and the range to be $\left\{g\right(x):g(x)\in [2,\infty \left)\right\}$ .

The $y$ -intercept is $y_{int}=5$ and there are no $x$ -intercepts.