4.3 Quadratic concepts -- solving quadratic equations by completing

Consider the equation:

We can solve this by analogy to the way that we approached absolute value problems. something squared is 16. So what could the something be? It could be 4. It could also be $-4$ . So the solution is:

• $x+3=4$
  • $x=1$
• $x+3=-4$
  • $x=-7$

These are the two solutions.

This simple problem leads to a completely general way of solving quadratic equations—because any quadratic equation can be put in a form like the above equation. The key is completing the square which, in turn, is based on our original two formulae:

As an example, consider the equation $x^2+\text{10}x+\text{21}=0$ . In order to make it fit one of the patterns above, we must replace the 21 with the correct number: a number such that $x^2+\text{10}x+\text{\_\_}$ is a perfect square. What number goes there? If you are familiar with the pattern, you know the answer right away. 10 is 5 doubled , so the number there must be 5 squared , or 25.

But how do we turn a 21 into a 25? We add 4, of course. And if we add 4 to one side of the equation, we have to add 4 to the other side of the equation. So the entire problem is worked out as follows:

Thus, we have our two solutions.

Completing the square is more time-consuming than factoring: so whenever a quadratic equation can be factored, factoring is the preferred method. (In this case, we would have factored the original equation as $\left(x+3\right)\left(x+7\right)$ and gotten straight to the answer.) However, completing the square can be used on any quadratic equation. In the example below, completing the square is used to find two answers that would not have been found by factoring.

Two steps in particular should be pointed out here.

In the third step, we divide both sides by 9. When completing the square, you do not want to have any coefficient in front of the term; if there is a number there, you divide it out. Fractions, on the other hand (such as the $-\frac{\text{80}}{9}$ in this case) do not present a problem. This is in marked contrast to factoring, where a coefficient in front of the $x^2$ can be left alone, but fractions make things nearly impossible.

The step after that is where we actually complete the square. $x^2+\mathrm{6x}+\text{\_\_}$ will be our perfect square. How do we find what number we want? Start with the coefficient of $x^2$ (in this case, 6). Take half of it, and square the result . Half of 6 is 3, squared is 9. So we want a 9 there to create $x^2+\mathrm{6x}+9$ which can be simplified to ${\left(x+3\right)}^2$ .

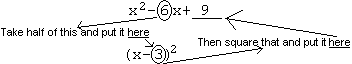
If the coefficient of $x$ is an odd number , the problem becomes a little uglier, but the principle is the same. For instance, faced with:

You would begin by taking half of 5 (which is $\frac{5}{2}$ ) and then squaring it:

$x^2+\mathrm{5x}+\frac{\text{25}}{4}={\left(x+\frac{5}{2}\right)}^2$

Another “completing the square” example, in which you cannot get rid of the square root at all, is presented in the worksheet “The Generic Quadratic Equation.”

One final note on completing the square: there are three different possible outcomes.

• If you end up with something like ${\left(x-3\right)}^2=\text{16}$ you will find two solutions, since $x-3$ can be either 4, or $-4$ . You will always have two solutions if the right side of the equation, after completing the square, is positive.
• If you end up with ${\left(x-3\right)}^2=0$ then there is only one solution: x must be 3 in this example. If the right side of the equation is 0 after completing the square, there is only one solution.
• Finally, what about a negative number on the right, such as ${\left(x-3\right)}^2=-\text{16}$ ? Nothing squared can give a negative answer, so there is no solution.