| << Chapter < Page | Chapter >> Page > |
MATHEMATICS
Grade 9
QUADRILATERALS, PERSPECTIVE DRAWING,TRANSFORMATIONS
Module 24
DRAWING PLAN AND SIDE VIEWS OF THREE-DIMENSIONAL OBJECTS TO SCALE
Putting three dimensions into two
ACTIVITY 1
To draw plan and side views of three-dimensional objects to scale
[LO 1.3, 3.4]
Orthographic projection
On the squared paper below you can see three drawings, each showing one side of a square wooden block with shaped holes in it.
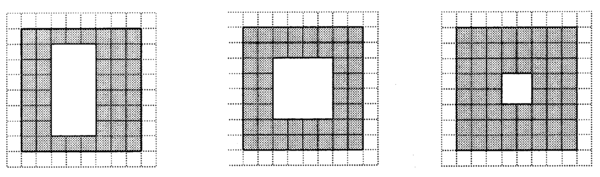
These are three orthographic views of the object. The drawings are done from the viewpoint of someone who is looking at the exact centre of each side of the block, with the line of sight perpendicular to the side. Ortho refers to 90°.
If each square on the paper represents 1 cm, calculate the outside dimensions of the block. Then calculate the total volume of wood removed in the making of the three different holes in the block.
These drawings give the dimensions of the object accurately to scale. This makes it possible for someone who has to manufacture or construct the object, to do it accurately. Architects use orthographic projections to make drawings of the plan of a building, as well as the views from the front and the sides. A builder needs to submit these drawings, as well as other technical specifications, to the people responsible for giving him permission to continue with the building.
Draw, as accurately as you can, the plan of your family’s house. If you can, also draw the front view of the house. Remember that you have to decide how many metres in the actual house will be represented by each centimetre in your drawing; this is the scale of your drawing.
ACTIVITY 2
To understand what the meaning and application of perspective drawings are
[LO 3.4]

Alongside is a three-dimensional drawing of the same block. You can read the dimensions
of the object from the drawing, just as in the orthographic drawings above, because iso
refers to the same and metric refers to measurement.
An isometric drawing is very useful, but it is not a good picture of what we would really
see if we had the block in front of our eyes. To give a more realistic view of the object,
we have to make a perspective drawing. This is discussed in the next section.
Here is some isometric paper for you to use.
Take one of your fat textbooks and draw an isometric projection of it. First determine a
good scale for your drawing.

ACTIVITY 3
To understand what the meaning and application of perspective drawings are
[LO 3.6]
One-point perspective projection
This is how you can make a perspective drawing on a window (use a marker pen that will wash off the glass when you have done, or stick transparent tracing paper to the glass). On the other side of the glass you have the object you want to draw – say you put a box on a table so that you can see it clearly fitting into the whole pane of glass. Don’t put the box perpendicular to the window, but put it with one corner facing forward. It is essential that you keep your head absolutely still while you work. Copy on the glass exactly what you see through the window, especially the edges of the box. You can compare your work with the explanation below, to see whether you have managed it well.
Of course, this is not what an architect does when he has to draw a picture of a building that still has to be built! He gives the orthographic projections that he has drawn to a draughtsperson who uses mathematical principles to make a perspective drawing of it.
There are one-point, two-point and three-point perspective drawings. This refers to the number of vanishing points in the drawing.
Here is a simple sketch in one-point perspective of a landscape with a railway line and a fence. There is one point on the horizon where all the lines in the sketch seem to meet and vanish.

In the sketch the railway sleepers, as well as the fence posts, seem to get closer to each other as they vanish into the distance; but we know that they are evenly spaced everywhere. The railway lines seem to get closer to each other as we move our eyes to the horizon. The distances between the sleepers, and between the fence posts, diminish in proportion to how far they are away from you. These effects create the illusion of three dimensions, even though the sketch is in two dimensions on a flat sheet of paper.
The next drawing is a perspective drawing of the square block that this section started with. As you can see, this shows a more realistic view of what the block really looks like in real life. The dotted lines show the horizon and the vanishing point.
The artist and architect Filippo Brunelleschi discovered how to use one-point perspective in the beginning of the fifteenth century.
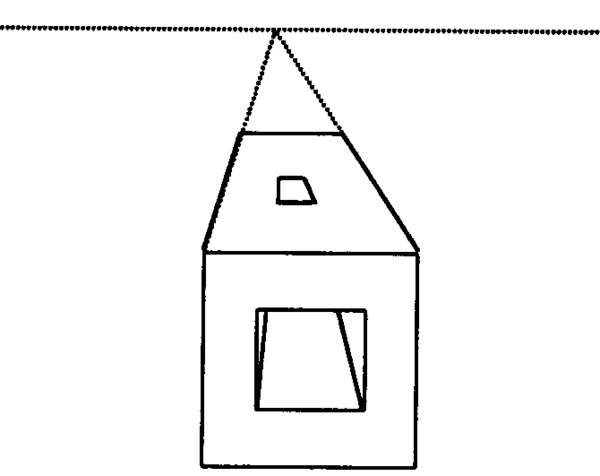
Attempt to draw a one-point perspective drawing of the block from the face of the block you can’t see in this drawing.
Assessment
| Learning outcomes(LOs) |
| LO 1 |
| Numbers, Operations and RelationshipsThe learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems. |
| Assessment standards(ASs) |
| We know this when the learner: |
| 1.3 solves problems in context including contexts that may be used to build awareness of other learning areas, as well as human rights, social, economic and environmental issues such as: |
| 1.3.2 measurements in Natural Sciences and Technology contexts. |
| LO 3 |
| Space and Shape (Geometry)The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three–dimensional objects in a variety of orientations and positions. |
| We know this when the learner: |
| 3.2 in contexts that include those that may be used to build awareness of social, cultural and environmental issues, describes the interrelationships of the properties of geometric figures and solids with justification, including: |
| 3.2.2 transformations. |
| 3.3 uses geometry of straight lines and triangles to solve problems and to justify relationships in geometric figures; |
| 3.4 draws and/or constructs geometric figures and makes models of solids in order to investigate and compare their properties and model situations in the environment; |
| 3.6 recognises and describes geometric solids in terms of perspective, including simple perspective drawing; |
| 3.7 uses various representational systems to describe position and movement between positions, including:ordered grids |

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?