1. Home
  2. Ut austin - principles of
  3. Physical states
  4. The separate & Ideal gas laws

4.2 The separate & Ideal gas laws  (Page 47/19)

<< Chapter < Page
  Ut austin - principles of     Page 1 / 19
Chapter >> Page >
By the end of this section, you will be able to:
  • Identify the mathematical relationships between the various properties of gases
  • Use the ideal gas law, and related gas laws, to compute the values of various gas properties under specified conditions

During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could fly ( [link] ), a number of scientists established the relationships between the macroscopic physical properties of gases, that is, pressure, volume, temperature, and amount of gas. Although their measurements were not precise by today’s standards, they were able to determine the mathematical relationships between pairs of these variables (e.g., pressure and temperature, pressure and volume) that hold for an ideal gas—a hypothetical construct that real gases approximate under certain conditions. Eventually, these individual laws were combined into a single equation—the ideal gas law —that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships (for pedagogical reasons not quite in historical order), then put them together in the ideal gas law.

This figure includes three images. Image a is a black and white image of a hydrogen balloon apparently being deflated by a mob of people. In image b, a blue, gold, and red balloon is being held to the ground with ropes while positioned above a platform from which smoke is rising beneath the balloon. In c, an image is shown in grey on a peach-colored background of an inflated balloon with vertical striping in the air. It appears to have a basket attached to its lower side. A large stately building appears in the background.
In 1783, the first (a) hydrogen-filled balloon flight, (b) manned hot air balloon flight, and (c) manned hydrogen-filled balloon flight occurred. When the hydrogen-filled balloon depicted in (a) landed, the frightened villagers of Gonesse reportedly destroyed it with pitchforks and knives. The launch of the latter was reportedly viewed by 400,000 people in Paris.

Pressure and temperature: amontons’s law

Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter ( [link] ) and the pressure increases.

This figure includes three similar diagrams. In the first diagram to the left, a rigid spherical container of a gas to which a pressure gauge is attached at the top is placed in a large beaker of water, indicated in light blue, atop a hot plate. The needle on the pressure gauge points to the far left on the gauge. The diagram is labeled “low P” above and “hot plate off” below. The second similar diagram also has the rigid spherical container of gas placed in a large beaker from which light blue wavy line segments extend from the top of the liquid in the beaker. The beaker is situated on top of a slightly reddened circular area. The needle on the pressure gauge points straight up, or to the middle on the gauge. The diagram is labeled “medium P” above and “hot plate on medium” below. The third diagram also has the rigid spherical container of gas placed in a large beaker in which bubbles appear near the liquid surface and several wavy light blue line segments extend from the surface out of the beaker. The beaker is situated on top of a bright red circular area. The needle on the pressure gauge points to the far right on the gauge. The diagram is labeled “high P” above and “hot plate on high” below.
The effect of temperature on gas pressure: When the hot plate is off, the pressure of the gas in the sphere is relatively low. As the gas is heated, the pressure of the gas in the sphere increases.

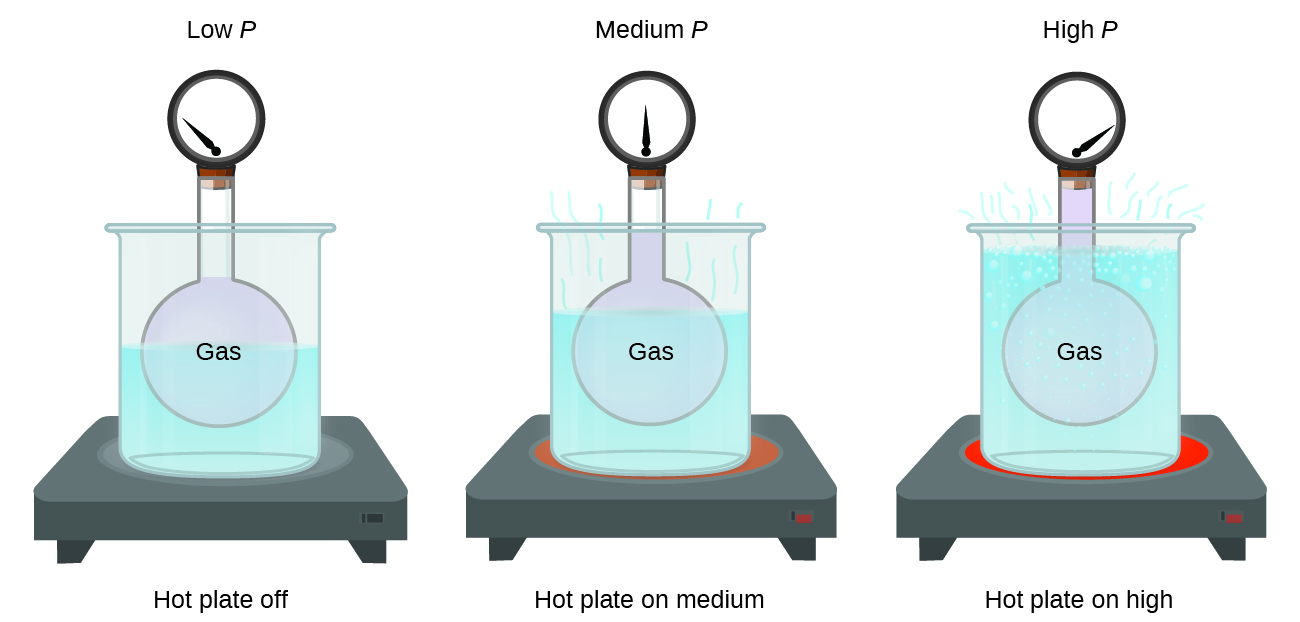
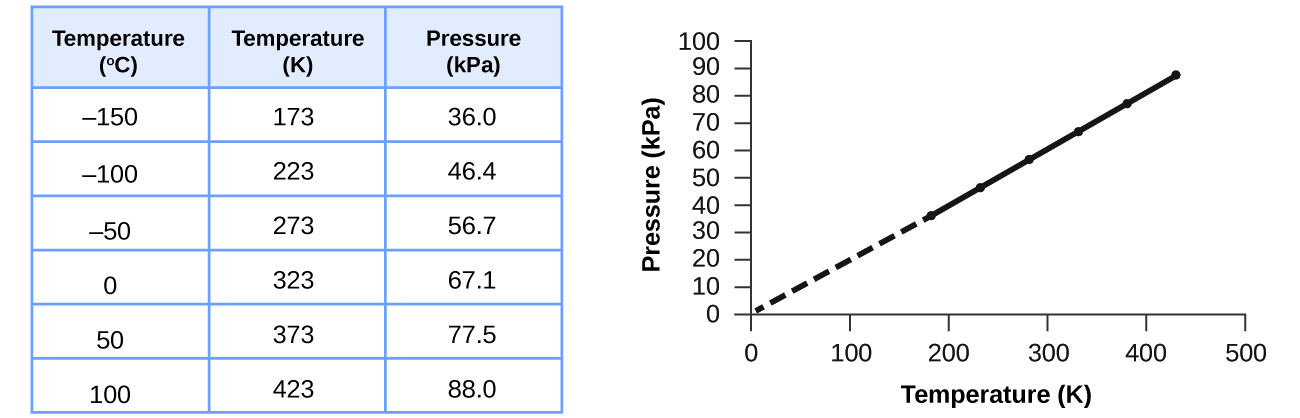
This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in [link] . We find that temperature and pressure are linearly related, and if the temperature is on the kelvin scale, then P and T are directly proportional (again, when volume and moles of gas are held constant ); if the temperature on the kelvin scale increases by a certain factor, the gas pressure increases by the same factor.

This figure includes a table and a graph. The table has 3 columns and 7 rows. The first row is a header, which labels the columns “Temperature, degrees C,” “Temperature, K,” and “Pressure, k P a.” The first column contains the values from top to bottom negative 150, negative 100, negative 50, 0, 50, and 100. The second column contains the values from top to bottom 173, 223, 273, 323, 373, and 423. The third column contains the values 36.0, 46.4, 56.7, 67.1, 77.5, and 88.0. A graph appears to the right of the table. The horizontal axis is labeled “Temperature ( K ).” with markings and labels provided for multiples of 100 beginning at 0 and ending at 500. The vertical axis is labeled “Pressure ( k P a )” with markings and labels provided for multiples of 10, beginning at 0 and ending at 100. Six data points from the table are plotted on the graph with black dots. These dots are connected with a solid black line. A dashed line extends from the data point furthest to the left to the origin. The graph shows a positive linear trend.
For a constant volume and amount of air, the pressure and temperature are directly proportional, provided the temperature is in kelvin. (Measurements cannot be made at lower temperatures because of the condensation of the gas.) When this line is extrapolated to lower pressures, it reaches a pressure of 0 at –273 °C, which is 0 on the kelvin scale and the lowest possible temperature, called absolute zero.

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 10

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Ut austin - principles of chemistry. OpenStax CNX. Mar 31, 2016 Download for free at http://legacy.cnx.org/content/col11830/1.13
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Ut austin - principles of chemistry' conversation and receive update notifications?

Ask