| << Chapter < Page | Chapter >> Page > |
Explain the relationship between the Pythagorean Theorem and the Law of Cosines.
When must you use the Law of Cosines instead of the Pythagorean Theorem?
The Law of Cosines must be used for any oblique (non-right) triangle.
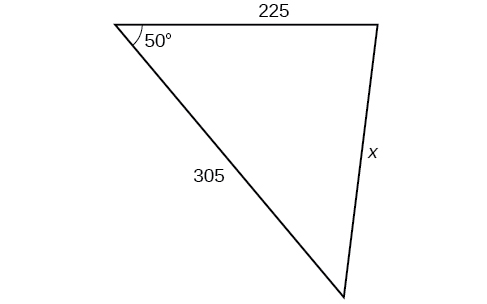
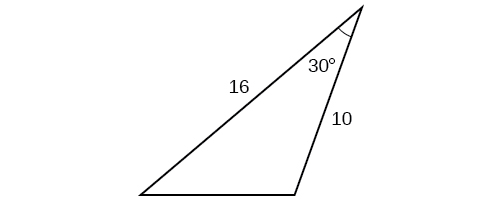
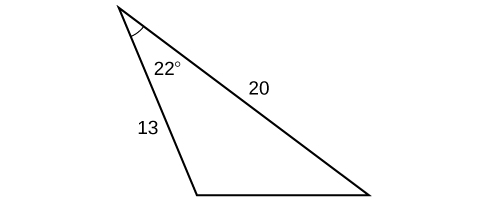
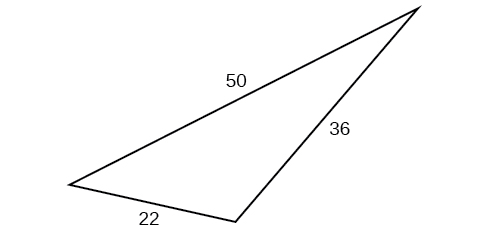
For the following exercises, assume is opposite side is opposite side and is opposite side If possible, solve each triangle for the unknown side. Round to the nearest tenth.
11.3
34.7
26.7
257.4
not possible
For the following exercises, use the Law of Cosines to solve for the missing angle of the oblique triangle. Round to the nearest tenth.
find angle
find angle
95.5°
find angle
find angle
26.9°
find angle
For the following exercises, solve the triangle. Round to the nearest tenth.
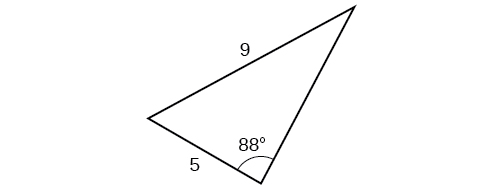
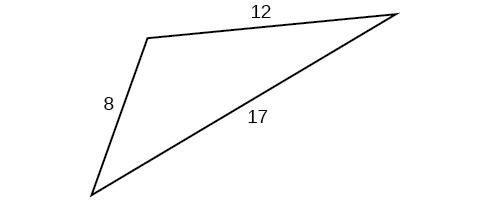
For the following exercises, use Heron’s formula to find the area of the triangle. Round to the nearest hundredth.
Find the area of a triangle with sides of length 18 in, 21 in, and 32 in. Round to the nearest tenth.
177.56 in 2
Find the area of a triangle with sides of length 20 cm, 26 cm, and 37 cm. Round to the nearest tenth.
0.04 m 2
0.91 yd 2
For the following exercises, find the length of side Round to the nearest tenth.
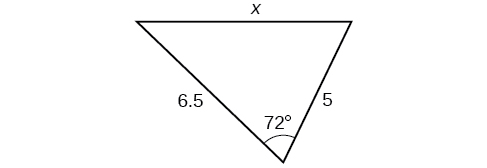
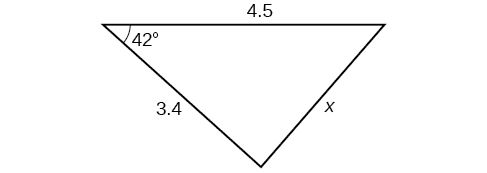
3.0
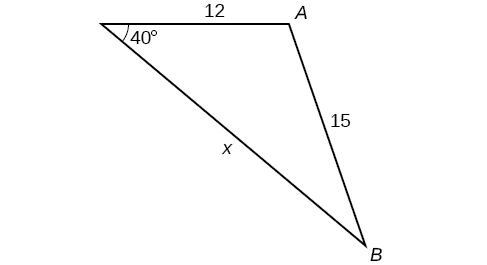
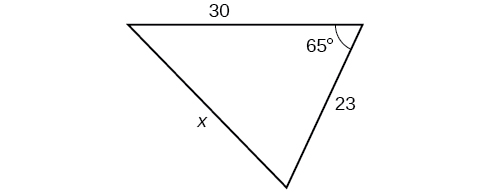
29.1
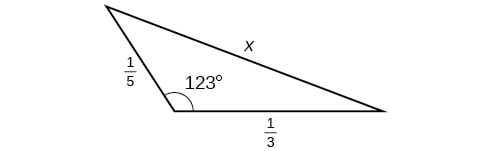
0.5
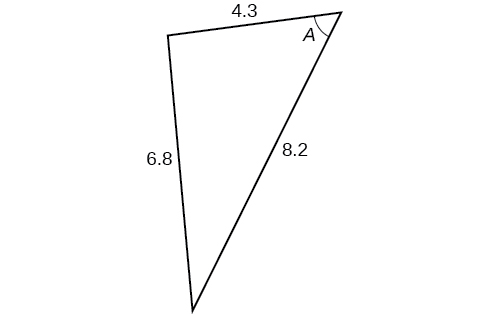
For the following exercises, find the measurement of angle
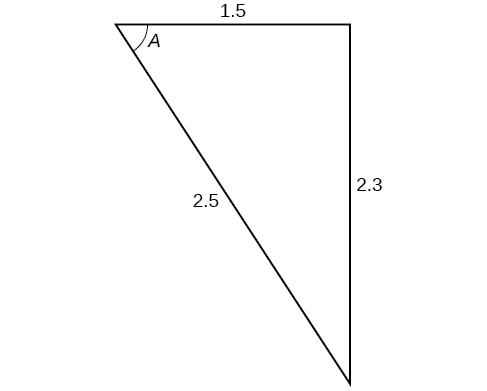
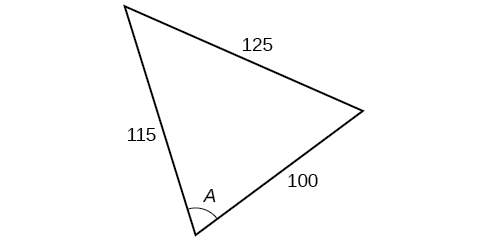
70.7°
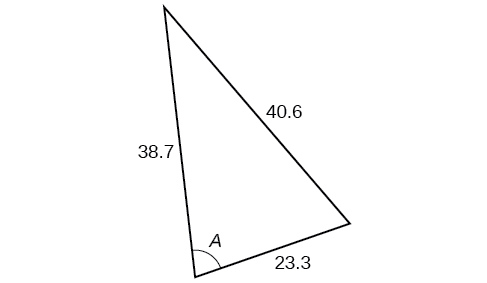
77.4°
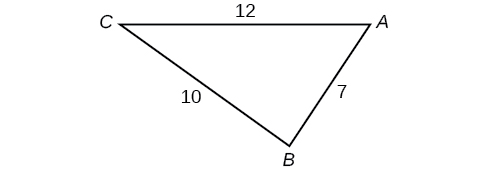
Find the measure of each angle in the triangle shown in [link] . Round to the nearest tenth.
For the following exercises, solve for the unknown side. Round to the nearest tenth.
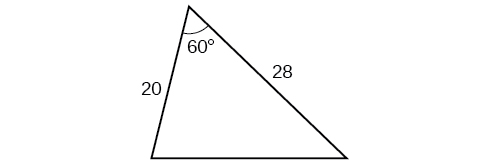
25.0
9.3
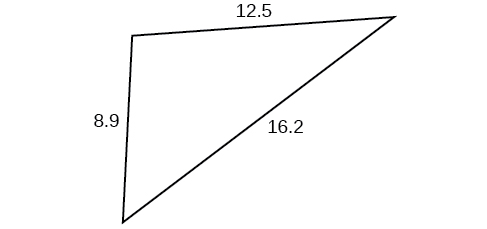
For the following exercises, find the area of the triangle. Round to the nearest hundredth.
43.52
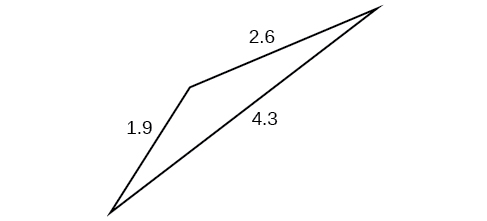
1.41
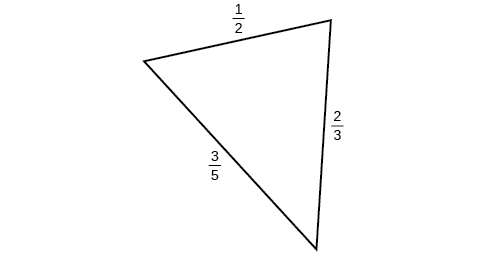
0.14
A parallelogram has sides of length 16 units and 10 units. The shorter diagonal is 12 units. Find the measure of the longer diagonal.
The sides of a parallelogram are 11 feet and 17 feet. The longer diagonal is 22 feet. Find the length of the shorter diagonal.
18.3
The sides of a parallelogram are 28 centimeters and 40 centimeters. The measure of the larger angle is 100°. Find the length of the shorter diagonal.
A regular octagon is inscribed in a circle with a radius of 8 inches. (See [link] .) Find the perimeter of the octagon.
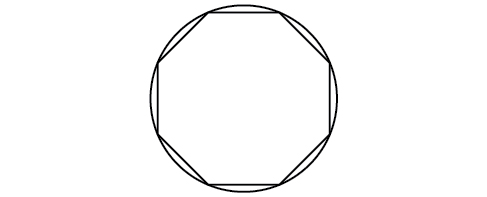
48.98
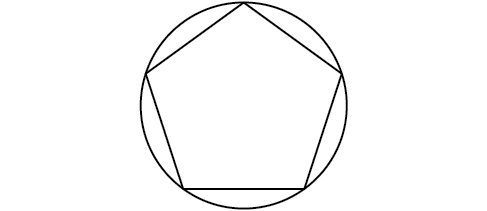
A regular pentagon is inscribed in a circle of radius 12 cm. (See [link] .) Find the perimeter of the pentagon. Round to the nearest tenth of a centimeter.
For the following exercises, suppose that represents the relationship of three sides of a triangle and the cosine of an angle.
Draw the triangle.
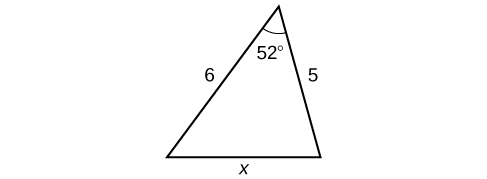
Find the length of the third side.
For the following exercises, find the area of the triangle.

7.62

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?