4.19 Probability  (Page 2/2)

b) Now throw the di 15 times. In the space below make a tick (√) every time the 3 lands on top.

Now write the total number of ticks as a fraction where the denominator is 15. _____________________________________________________________________

Is your answer close to one sixth (use your calculator) _________________________

Can you explain this? __________________________________________________

_____________________________________________________________________

20.5 Did you know?

It would be pure chance if you achieved a probability of one sixth in the above activity. Practical probability is based on what you actually did. Theoretical probability is only an attempt to predict what might happen.

The more times that you throw the di, the closer the practical

and theoretical probabilities should come to each other.

20.6 BRAINTEASER

• What is the probability that you will get 7, if you throw two dice at the same time and add the numbers that are showing upwards?

_____________________________________________________________________

_____________________________________________________________________

21. Time for self-assessment

Colour in the face that is true of you:
I can explain the concept “probability”.
I know what a probability of 0 means.
know what a probability of 1 means.
I know the “formula” to determine probability.
I was able to correctly calculate the probability in the given questions.

22. For FUN!

• Use the given co-ordinates and decode the code:

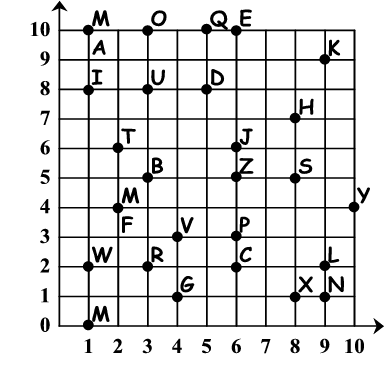
(9,9) (9,2) (1,10) (1,10) (3,2) (1,0) (6,10) (2,6)

............................................ .........................

(4,1) (3,2) (1,10) (1,10) (5,8) (8,5) (6,10) (1,2) (6,10)

............................................ ......................................

(8,5) (6,10) (1,2) (1,8) (8,5) (9,9) (3,8) (9,1) (5,8) (6,10)!!

................. ......................................................................!!

Assessment

Learning Outcome 5: The learner will be able to collect, summarise, display and critically analyse data in order to draw conclusions and make predictions, and to interpret and determine chance variation.

Assessment Standard 5.9: We know this when the learner critically reads and interprets data presented in a variety of ways to draw conclusions and make predictions sensitive.

Assessment Standard 5.10: We know this when the learner performs simple experiments where the possible outcomes are equally likely.

Module test

1. Reduce the frog on a scale 2:1.

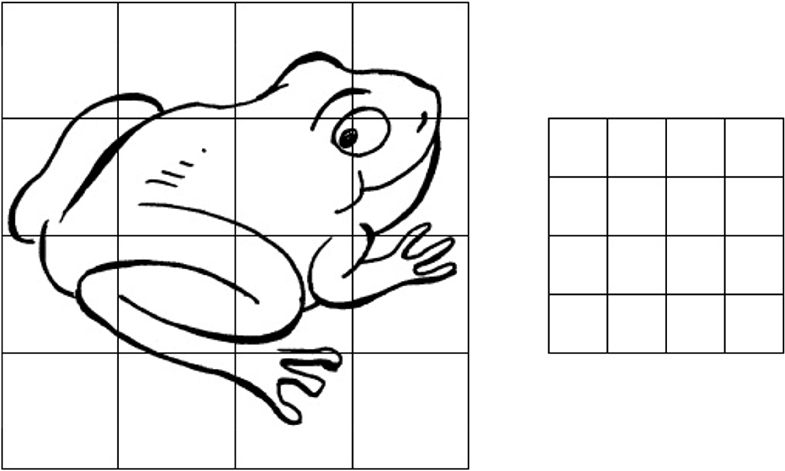
(3)

2. What kind of transformation was in the following figure?

_____________________________________________

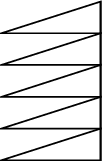
(1)

3. Explain the following concepts:

a) random test: ____________________________________________________

_____________________________________________________________________

_____________________________________________________________________

(2)

b) probability: _____________________________________________________

_____________________________________________________________________

_____________________________________________________________________

(2)

4. Look at the following:

A group of learners’ marks out of 15 were as follows:

6; 11 ; 12 ; 15 ; 9 ; 10 ; 10 ; 10 ; 8 ; 15

a) Calculate the mode:_______________________________________________

_____________________________________________________________________

_____________________________________________________________________

(2)

b) Calculate the median: _____________________________________________

_____________________________________________________________________

_____________________________________________________________________

(2)

c) Calculate the arithmetic mean (average): ______________________________

_____________________________________________________________________

_____________________________________________________________________

(2)

5. Study the graph and answer the following questions:

a) What is this type of graph called?

_____________________________________________________________________

(1)

b) Why does it “jump” from 0 to 6?

_____________________________________________________________________

_____________________________________________________________________

(1)

c) How many learners are 7 years old?

_____________________________________________________________________

(1)

d) How many more 9 year old learners are there than 12 year olds?

_____________________________________________________________________

(1)

e) How many learners are there in the school?

_____________________________________________________________________

(1)

6. Represent the information given in question on a line graph.

(3)

7. What is the probability that you will take a black ball from a container containing 12 red, 6 green, 4 black, 2 yellow and 8 blue balls?

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

(2)