| << Chapter < Page | Chapter >> Page > |
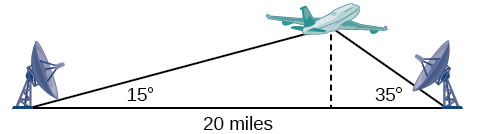
Suppose two radar stations located 20 miles apart each detect an aircraft between them. The angle of elevation measured by the first station is 35 degrees, whereas the angle of elevation measured by the second station is 15 degrees. How can we determine the altitude of the aircraft? We see in [link] that the triangle formed by the aircraft and the two stations is not a right triangle, so we cannot use what we know about right triangles. In this section, we will find out how to solve problems involving non-right triangles .
In any triangle, we can draw an altitude , a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.
Any triangle that is not a right triangle is an oblique triangle . Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:
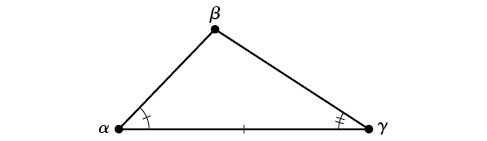
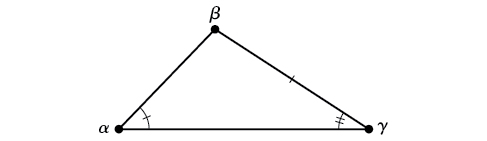
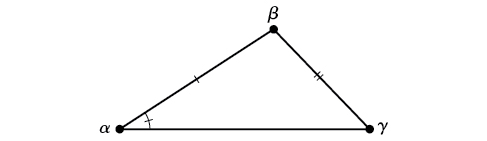
Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in [link] .
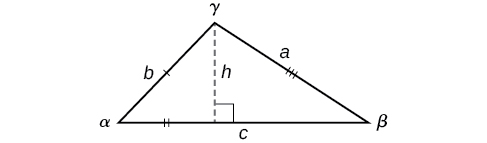
Using the right triangle relationships, we know that and Solving both equations for gives two different expressions for
We then set the expressions equal to each other.
Similarly, we can compare the other ratios.
Collectively, these relationships are called the Law of Sines .
Note the standard way of labeling triangles: angle (alpha) is opposite side angle (beta) is opposite side and angle (gamma) is opposite side See [link] .
While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.
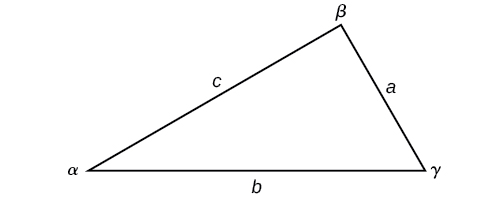
Given a triangle with angles and opposite sides labeled as in [link] , the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.
To solve an oblique triangle, use any pair of applicable ratios.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?