Home
Advanced algebra ii: activities Quadratics Homework: multiplying binomials
Some homework problems on multiplying binomials.
Memorize these:
(
x
+
a
)
2
=
x
2
+
2
ax
+
a
2
size 12{ \( x+a \) rSup { size 8{2} } =x rSup { size 8{2} } +2 ital "ax"+a rSup { size 8{2} } } {}
(
x
−
a
)
2
=
x
2
−
2
ax
+
a
2
size 12{ \( x - a \) rSup { size 8{2} } =x rSup { size 8{2} } - 2 ital "ax"+a rSup { size 8{2} } } {}
x
2
−
a
2
=
(
x
+
a
)
(
x
−
a
)
size 12{x rSup { size 8{2} } - a rSup { size 8{2} } = \( x+a \) \( x - a \) } {}
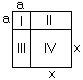
In the following drawing, one large square is divided into four regions. The four small regions are labeled with Roman numerals because I like to show off.
a How long is the left side of the entire figure? _______________
b How long is the bottom of the entire figure? _______________
c One way to compute the area of the entire figure is to multiply these two numbers (total height times total width). Write this product down here: Area = _______________
d Now: what is the area of the small region labeled I? _______________
e What is the area of the small region labeled II? _______________
f What is the area of the small region labeled III? _______________
g What is the area of the small region labeled IV? _______________
h The other way to compute the area of the entire figure is to add up these small regions. Write this sum down here: Area =_________________
i Obviously, the answer to (c) and the answer to (h) have to be the same, since they are both the area of the entire figure. So write down the equation setting these two equal to each other here: ____________________________________
j that look like one of our three formulae? Got questions? Get instant answers now!
Multiply these out “manually.”
a
(
x
+
3
)
(
x
+
4
)
size 12{ \( x+3 \) \( x+4 \) } {}
b
(
x
+
3
)
(
x
−
4
)
size 12{ \( x+3 \) \( x - 4 \) } {}
c
(
x
−
3
)
(
x
−
4
)
size 12{ \( x - 3 \) \( x - 4 \) } {}
d
(
2x
+
3
)
(
3x
+
2
)
size 12{ \( 2x+3 \) \( 3x+2 \) } {}
e
(
x
−
2
)
(
x
2
+
2x
+
4
)
size 12{ \( x - 2 \) \( x rSup { size 8{2} } +2x+4 \) } {}
f Check your answer to part (e) by substituting the number 3 into both my original function, and your answer. Do they come out the same? Got questions? Get instant answers now!
Multiply these out using the formulae above.
a
(
x
+
3
/
2
)
2
size 12{ \( x+ {3} slash {2} \) rSup { size 8{2} } } {}
b
(
x
−
3
/
2
)
2
size 12{ \( x - {3} slash {2} \) rSup { size 8{2} } } {}
c
(
x
+
3
)
2
size 12{ \( x+3 \) rSup { size 8{2} } } {}
d
(
3
+
x
)
2
size 12{ \( 3+x \) rSup { size 8{2} } } {}
e
(
x
−
3
)
2
size 12{ \( x - 3 \) rSup { size 8{2} } } {}
f
(
3
−
x
)
2
size 12{ \( 3 - x \) rSup { size 8{2} } } {}
g Hey, why did (e) and (f) come out the same? (
x
−
3
size 12{x - 3} {} isn’t the same as
3
−
x
size 12{3 - x} {} , is it?)
h
(
x
+
1
/
2
)
(
x
+
1
/
2
)
size 12{ \( x+ {1} slash {2} \) \( x+ {1} slash {2 \) } } {}
i
(
x
+
1
/
2
)
(
x
−
1
/
2
)
size 12{ \( x+ {1} slash {2} \) \( x - {1} slash {2 \) } } {}
j
(
5
−
3
)
(
5
+
3
)
size 12{ \( sqrt {5} - sqrt {3} \) \( sqrt {5} + sqrt {3} \) } {}
k Check your answer to part (j) by running through the whole calculation on your calculator:
5
−
3
=
size 12{ sqrt {5} - sqrt {3} ={}} {} _______,
5
+
3
=
size 12{ sqrt {5} + sqrt {3} ={}} {} _______, multiply them and you get _______. Got questions? Get instant answers now!
Now, let’s try going
backward . Rewrite the following expressions as
(
x
+
something
)
2
size 12{ \( x+"something" \) rSup { size 8{2} } } {} , or as
(
x
−
something
)
2
size 12{ \( x - "something" \) rSup { size 8{2} } } {} , or as
(
x
+
something
)
(
x
−
something
)
size 12{ \( x+"something" \) \( x - "something" \) } {} . In each case, check your answer by multiplying back to see if you get the original expression.
a
x
2
−
8x
+
16
=
size 12{x rSup { size 8{2} } - 8x+"16"={}} {} ____________
Check by multiplying back: _______________
b
x
2
−
25
=
size 12{x rSup { size 8{2} } - "25"={}} {} ____________
Check by multiplying back: _______________
c
x
2
+
2x
+
1
=
size 12{x rSup { size 8{2} } +2x+1={}} {} ____________
Check by multiplying back: _______________
d
x
2
−
20
x
+
100
=
size 12{x rSup { size 8{2} } - "20"x+"100"={}} {} ____________
Check by multiplying back: _______________
e
4x
2
−
9
=
size 12{4x rSup { size 8{2} } - 9={}} {} ____________
Check by multiplying back: _______________ Got questions? Get instant answers now!
Enough squaring: let’s go one higher, and see what
(
x
+
a
)
3
size 12{ \( x+a \) rSup { size 8{3} } } {} is!
a
(
x
+
a
)
3
size 12{ \( x+a \) rSup { size 8{3} } } {} means (
(
x
+
a
)
(
x
+
a
)
(
x
+
a
)
size 12{ \( x+a \) \( x+a \) \( x+a \) } {} . You already know what
(
x
+
a
)
(
x
+
a
)
size 12{ \( x+a \) \( x+a \) } {} is. So multiply
that by
(
x
+
a
)
size 12{ \( x+a \) } {} to find the cubed formula. (Multiply term-by-term, then collect like terms.)
b
Use the formula you just found to find
(
y
+
a
)
3
size 12{ \( y+a \) rSup { size 8{3} } } {} .
c Use the same formula to find
(
y
−
3
)
3
size 12{ \( y - 3 \) rSup { size 8{3} } } {} . Got questions? Get instant answers now!
Source:
OpenStax, Advanced algebra ii: activities and homework. OpenStax CNX. Sep 15, 2009 Download for free at http://cnx.org/content/col10686/1.5
Google Play and the Google Play logo are trademarks of Google Inc.