30.4 Nuclear decay and conservation laws  (Page 4/25)

If a nuclide ${}_Z^A{\mathrm{X}}_N$ is known to ${\beta }^{-}$ decay, then its ${\beta }^{-}$ decay equation is

where Y is the nuclide having one more proton than X (see [link] ). So if you know that a certain nuclide ${\beta }^{-}$ decays, you can find the daughter nucleus by first looking up $Z$ for the parent and then determining which element has atomic number $Z+1$ . In the example of the ${\beta }^{-}$ decay of ${}^{\text{60}}\text{Co}$ given earlier, we see that $Z=\text{27}$ for Co and $Z=\text{28}$ is Ni. It is as if one of the neutrons in the parent nucleus decays into a proton, electron, and neutrino. In fact, neutrons outside of nuclei do just that—they live only an average of a few minutes and ${\beta }^{-}$ decay in the following manner:

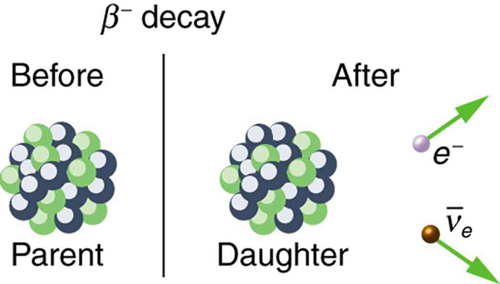
We see that charge is conserved in ${\beta }^{-}$ decay, since the total charge is $Z$ before and after the decay. For example, in ${}^{\text{60}}\text{Co}$ decay, total charge is 27 before decay, since cobalt has $Z=\text{27}$ . After decay, the daughter nucleus is Ni, which has $Z=\text{28}$ , and there is an electron, so that the total charge is also $\mathrm{28\; +\; (–1)}$ or 27. Angular momentum is conserved, but not obviously (you have to examine the spins and angular momenta of the final products in detail to verify this). Linear momentum is also conserved, again imparting most of the decay energy to the electron and the antineutrino, since they are of low and zero mass, respectively. Another new conservation law is obeyed here and elsewhere in nature. The total number of nucleons $A$ is conserved . In ${}^{\text{60}}\text{Co}$ decay, for example, there are 60 nucleons before and after the decay. Note that total $A$ is also conserved in $\alpha$ decay. Also note that the total number of protons changes, as does the total number of neutrons, so that total $Z$ and total $N$ are not conserved in ${\beta }^{-}$ decay, as they are in $\alpha$ decay. Energy released in ${\beta }^{-}$ decay can be calculated given the masses of the parent and products.