| << Chapter < Page | Chapter >> Page > |
Another radiation detection method records light produced when radiation interacts with materials. The energy of the radiation is sufficient to excite atoms in a material that may fluoresce, such as the phosphor used by Rutherford’s group. Materials called scintillators use a more complex collaborative process to convert radiation energy into light. Scintillators may be liquid or solid, and they can be very efficient. Their light output can provide information about the energy, charge, and type of radiation. Scintillator light flashes are very brief in duration, enabling the detection of a huge number of particles in short periods of time. Scintillator detectors are used in a variety of research and diagnostic applications. Among these are the detection by satellite-mounted equipment of the radiation from distant galaxies, the analysis of radiation from a person indicating body burdens, and the detection of exotic particles in accelerator laboratories.
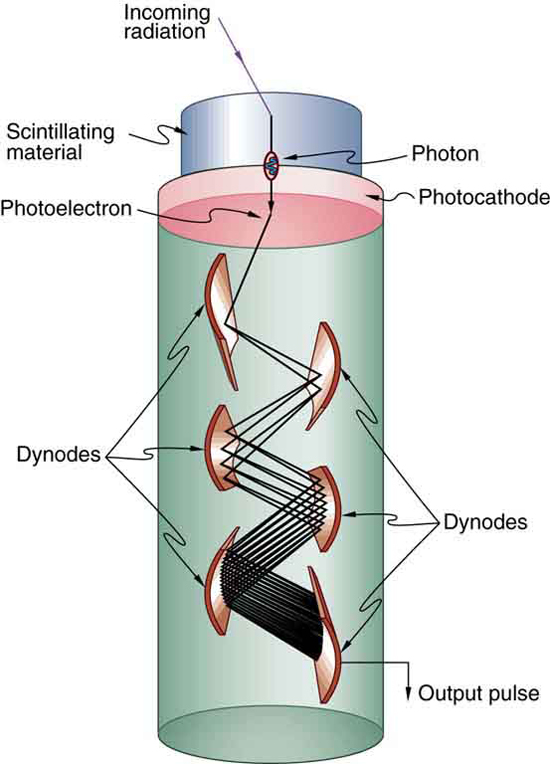
Light from a scintillator is converted into electrical signals by devices such as the photomultiplier tube shown schematically in [link] . These tubes are based on the photoelectric effect, which is multiplied in stages into a cascade of electrons, hence the name photomultiplier. Light entering the photomultiplier strikes a metal plate, ejecting an electron that is attracted by a positive potential difference to the next plate, giving it enough energy to eject two or more electrons, and so on. The final output current can be made proportional to the energy of the light entering the tube, which is in turn proportional to the energy deposited in the scintillator. Very sophisticated information can be obtained with scintillators, including energy, charge, particle identification, direction of motion, and so on.
Solid-state radiation detectors convert ionization produced in a semiconductor (like those found in computer chips) directly into an electrical signal. Semiconductors can be constructed that do not conduct current in one particular direction. When a voltage is applied in that direction, current flows only when ionization is produced by radiation, similar to what happens in a Geiger tube. Further, the amount of current in a solid-state detector is closely related to the energy deposited and, since the detector is solid, it can have a high efficiency (since ionizing radiation is stopped in a shorter distance in solids fewer particles escape detection). As with scintillators, very sophisticated information can be obtained from solid-state detectors.
Learn about different types of radiometric dating, such as carbon dating. Understand how decay and half life work to enable radiometric dating to work. Play a game that tests your ability to match the percentage of the dating element that remains to the age of the object.

Is it possible for light emitted by a scintillator to be too low in frequency to be used in a photomultiplier tube? Explain.
The energy of 30.0 is required to ionize a molecule of the gas inside a Geiger tube, thereby producing an ion pair. Suppose a particle of ionizing radiation deposits 0.500 MeV of energy in this Geiger tube. What maximum number of ion pairs can it create?
A particle of ionizing radiation creates 4000 ion pairs in the gas inside a Geiger tube as it passes through. What minimum energy was deposited, if 30.0 is required to create each ion pair?
(a) Repeat [link] , and convert the energy to joules or calories. (b) If all of this energy is converted to thermal energy in the gas, what is its temperature increase, assuming of ideal gas at 0.250-atm pressure? (The small answer is consistent with the fact that the energy is large on a quantum mechanical scale but small on a macroscopic scale.)
Suppose a particle of ionizing radiation deposits 1.0 MeV in the gas of a Geiger tube, all of which goes to creating ion pairs. Each ion pair requires 30.0 eV of energy. (a) The applied voltage sweeps the ions out of the gas in . What is the current? (b) This current is smaller than the actual current since the applied voltage in the Geiger tube accelerates the separated ions, which then create other ion pairs in subsequent collisions. What is the current if this last effect multiplies the number of ion pairs by 900?

Notification Switch
Would you like to follow the 'College physics -- hlca 1104' conversation and receive update notifications?