| << Chapter < Page | Chapter >> Page > |
1.1 22 m + 11 m + 33 m + 40 m + 28 m + 68 m = 202 m
1.2 202 poles
2. 112 m × 75 m = 8 400 m²
Cost: 8 400 × R1,20 = R10 080
3. 45 m × 45 m = 2 025 m²
R56 679,75 ÷ 2 025 = R27,99/m²
4. 225 cm × 75 cm = 16 875 cm²
2,25 m × 0,75 m = 1,6875 m²
5. 50,32 m² ÷ 7,4 m = 6,8 m
You have to divide into groups of three for this activity. You may use pocket calculators for solving the problems. Work neatly and show clearly how you go about to find the answers. Enjoy puzzling it out!
1. A farmer has to fence a paddock containing calves.
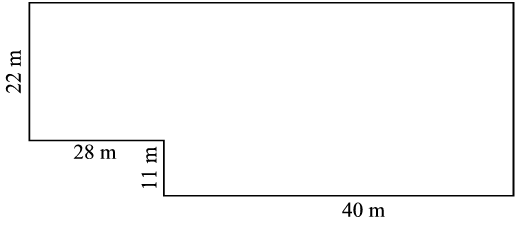
1.1 Calculate how much wire is needed to fence the paddock.
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
1.2 If the poles for the fence are planted 1 m apart, how many poles are required?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
2. Grass seed has to be sown on the new hockey field. The field is 112 m by 75 m. If the seed costs R1,20 per m2, what will the cost for the whole project be?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
3. If a square playing field with a length of 45 m is tarred, the total cost is R56 679,75. What is the cost of the tar per 1 m2?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
4. A portion of a bathroom wall of 2,25 m by 0,75 m must be covered by new tiles. The tiles are square, with a length of 15 cm. How many tiles are required?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
5. A classroom has an area of 50,32 m2. If the length is 7,4 m, what is the width?
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
ASSESSMENT: PROBLEM SOLVING
| CRITERIA | CODE | |||
| Neatness and organisation | The work is untidy and is disorganised. | The work is organised but is difficult to read. | The work is neat and organised and easy to read. | Neat and clearly set out work; clearly legible. |
| Logical reasoning | There is very little evidence of logical reasoning | There is some evidence of logical reasoning | Effective mathematical reasoning was used. | Sophisticated logic and reasoning was used. |
| Correctness of calculations | All the answers are calculated incorrectly | Many mistakes occur. | Few mistakes occur. | All answers are correctly calculated. |
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.6: We know this when the learner solves problems in context including contexts that may be used to build awareness of other Learning Areas, as well as human rights, social, economic and environmental issues such as:
1.6.2: measurements in Natural Sciences and Technology contexts;
Learning Outcome 4: The learner will be able to use appropriate measuring units, instruments and formulae in a variety of contexts.
Assessment Standard 4.8: We know this when the learner investigates and approximates (alone and/or as a member of a group or team):
4.8.2: area of polygons (using square grids) in order to develop rules for calculating the area of squares and rectangles.

Notification Switch
Would you like to follow the 'Mathematics grade 6' conversation and receive update notifications?