| << Chapter < Page | Chapter >> Page > |
One of the primary motivating factors for utilizing the z-transform and analyzing the pole/zero plots is due to their relationship to the frequency responseof a discrete-time system. Based on the position of the poles and zeros, one can quickly determine the frequency response. This is aresult of the correspondence between the frequency response and the transfer function evaluated on the unit circle in thepole/zero plots. The frequency response, or DTFT, of the system is defined as:
Let us now look at several examples of determining the magnitude of the frequency response from the pole/zero plot ofa z-transform. If you have forgotten or are unfamiliar with pole/zero plots, please refer back to the Pole/Zero Plots module.
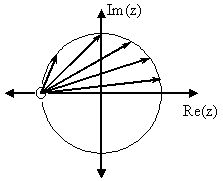
In this first example we will take a look at the very simple z-transform shown below: For this example, some of the vectors represented by , for random values of , are explicitly drawn onto the complex plane shown in the figure below. These vectors show how the amplitude of the frequency response changes as goes from to , and also show the physical meaning of the terms in [link] above. One can see that when , the vector is the longest and thus the frequency responsewill have its largest amplitude here. As approaches , the length of the vectors decrease as does the amplitude of . Since there are no poles in the transform, there is only this onevector term rather than a ratio as seen in [link] .

For this example, a more complex transfer function is analyzed in order to represent the system's frequencyresponse.
Below we can see the two figures described by the above equations. The [link] represents the basic pole/zero plot of the z-transform, . [link] shows the magnitude of the frequency response. From the formulas and statements in the previoussection, we can see that when the frequency will peak since it is at this value of that the pole is closest to the unit circle. The ratio from [link] helps us see the mathematics behindthis conclusion and the relationship between the distances from the unit circle and the poles and zeros. As moves from to , we see how the zero begins to mask the effects of the poleand thus force the frequency response closer to .
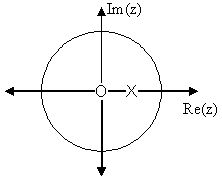

In conclusion, using the distances from the unit circle to the poles and zeros, we can plot the frequency response of thesystem. As goes from to , the following two properties, taken from the above equations, specify how one should draw .

Notification Switch
Would you like to follow the 'Intro to digital signal processing' conversation and receive update notifications?