| << Chapter < Page | Chapter >> Page > |
For the following exercises, find the inverse of the function and graph both the function and its inverse.
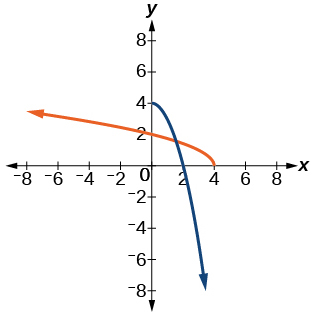
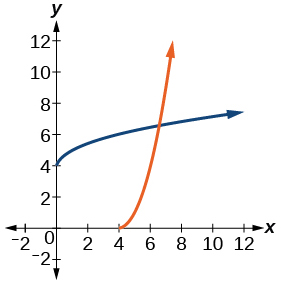
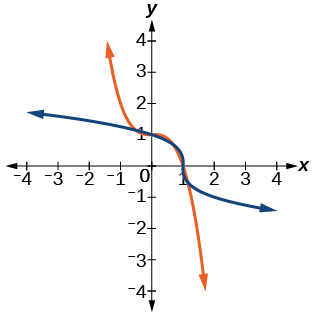
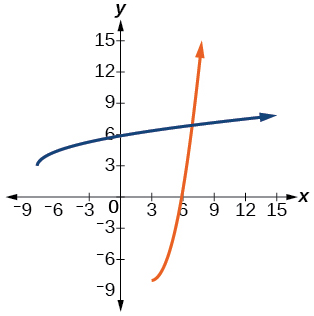
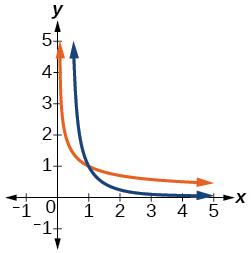
For the following exercises, use a graph to help determine the domain of the functions.
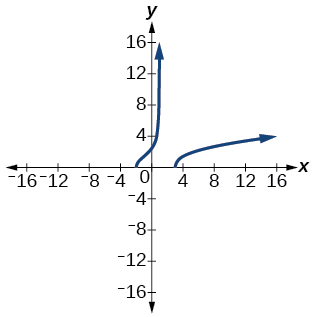
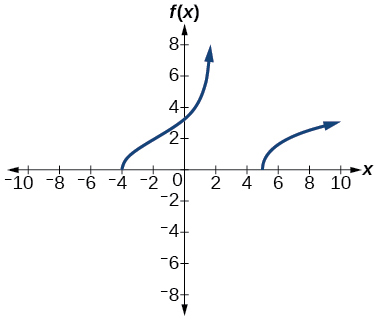
For the following exercises, use a calculator to graph the function. Then, using the graph, give three points on the graph of the inverse with y -coordinates given.
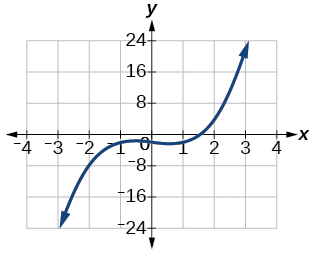
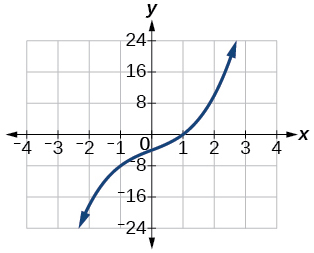
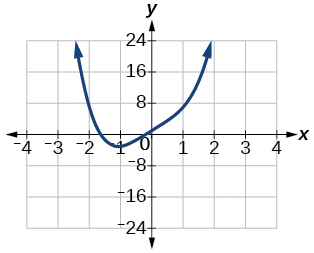
For the following exercises, find the inverse of the functions with positive real numbers.
For the following exercises, determine the function described and then use it to answer the question.
An object dropped from a height of 200 meters has a height, in meters after seconds have lapsed, such that Express as a function of height, and find the time to reach a height of 50 meters.
5.53 seconds
An object dropped from a height of 600 feet has a height, in feet after seconds have elapsed, such that Express as a function of height and find the time to reach a height of 400 feet.
The volume, of a sphere in terms of its radius, is given by Express as a function of and find the radius of a sphere with volume of 200 cubic feet.
3.63 feet
The surface area, of a sphere in terms of its radius, is given by Express as a function of and find the radius of a sphere with a surface area of 1000 square inches.
A container holds 100 ml of a solution that is 25 ml acid. If ml of a solution that is 60% acid is added, the function gives the concentration, as a function of the number of ml added, Express as a function of and determine the number of mL that need to be added to have a solution that is 50% acid.
250 mL
The period in seconds, of a simple pendulum as a function of its length in feet, is given by . Express as a function of and determine the length of a pendulum with period of 2 seconds.
The volume of a cylinder , in terms of radius, and height, is given by If a cylinder has a height of 6 meters, express the radius as a function of and find the radius of a cylinder with volume of 300 cubic meters.
3.99 meters
The surface area, of a cylinder in terms of its radius, and height, is given by If the height of the cylinder is 4 feet, express the radius as a function of and find the radius if the surface area is 200 square feet.
The volume of a right circular cone, in terms of its radius, and its height, is given by Express in terms of if the height of the cone is 12 feet and find the radius of a cone with volume of 50 cubic inches.
1.99 inches
Consider a cone with height of 30 feet. Express the radius, in terms of the volume, and find the radius of a cone with volume of 1000 cubic feet.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?