| << Chapter < Page | Chapter >> Page > |
If a function is not one-to-one, it cannot have an inverse. If we restrict the domain of the function so that it becomes one-to-one, thus creating a new function, this new function will have an inverse.
Given a polynomial function, restrict the domain of a function that is not one-to-one and then find the inverse.
Find the inverse function of
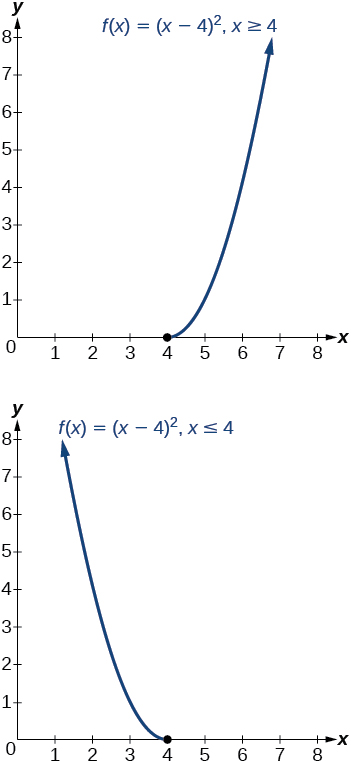
The original function is not one-to-one, but the function is restricted to a domain of or on which it is one-to-one. See [link] .
To find the inverse, start by replacing with the simple variable
This is not a function as written. We need to examine the restrictions on the domain of the original function to determine the inverse. Since we reversed the roles of and for the original we looked at the domain: the values could assume. When we reversed the roles of and this gave us the values could assume. For this function, so for the inverse, we should have which is what our inverse function gives.
Restrict the domain and then find the inverse of
We can see this is a parabola with vertex at that opens upward. Because the graph will be decreasing on one side of the vertex and increasing on the other side, we can restrict this function to a domain on which it will be one-to-one by limiting the domain to
To find the inverse, we will use the vertex form of the quadratic. We start by replacing with a simple variable, then solve for
Now we need to determine which case to use. Because we restricted our original function to a domain of the outputs of the inverse should be the same, telling us to utilize the + case
If the quadratic had not been given in vertex form, rewriting it into vertex form would be the first step. This way we may easily observe the coordinates of the vertex to help us restrict the domain.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?