| << Chapter < Page | Chapter >> Page > |
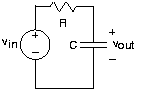
Let's consider a circuit having something other than resistors and sources. Because of KVL, we know that . The current through the capacitor is given by , and this current equals that passing through the resistor. Substituting into the KVL equation and using the v-i relation for the capacitor, we arrive at
At this point, we could learn how to solve differential equations. Note first that even finding the differentialequation relating an output variable to a source is often very tedious. The parallel and series combination rules that apply toresistors don't directly apply when capacitors and inductors occur. We would have to slog our way through the circuitequations, simplifying them until we finally found the equation that related the source(s) to the output. Atthe turn of the twentieth century, a method was discovered that not only made finding the differential equation easy, but also simplifiedthe solution process in the most common situation. Although not original with him, Charles Steinmetz presented the key paper describing the impedance approach in 1893. It allows circuits containing capacitors and inductors to be solved with the same methods we have learned to solved resistor circuits. To use impedances, we must master complex numbers . Though the arithmetic of complex numbers is mathematically more complicated than with real numbers, the increased insight into circuit behavior and the ease with which circuits are solved with impedances is well worth the diversion. But more importantly, the impedance concept is central to engineering and physics, having a reach far beyond just circuits.

Notification Switch
Would you like to follow the 'Fundamentals of electrical engineering i' conversation and receive update notifications?