-
Home
- Fundamentals of mathematics
- Exponents, roots, and factorization
- Summary of key concepts
This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module reviews the key concepts from the chapter "Exponents, Roots, Factorization of Whole Numbers."
Summary of key concepts
Exponential notation (
[link] )
Exponential notation is a description of repeated multiplication.
Exponent (
[link] )
An
exponent records the number of identical factors repeated in a multiplication.
In a number such as
,
7 is called the
base .
Exponent (
[link] )
3 is called the
exponent , or power.
is read "seven to the third power," or "seven cubed."
Squared, cubed (
[link] )
A number raised to the second power is often called
squared . A number raised to the third power is often called
cubed .
In mathematics, the word
root is used to indicate that, through repeated multiplication, one number is the source of another number.
The radical sign
(
[link] )
The symbol
is called a
radical sign and indicates the square root of a number. The symbol
represents the
th root.
Radical, index, radicand (
[link] )
An expression such as
is called a
radical and 4 is called the
index . The number 16 is called the
radicand .
Grouping symbols (
[link] )
Grouping symbols are used to indicate that a particular collection of numbers and meaningful operations are to be grouped together and considered as one number. The grouping symbols commonly used in mathematics are
- Parentheses: ( )
- Brackets: [ ]
- Braces: { }
- Bar:
Order of operations (
[link] )
- Perform all operations inside grouping symbols, beginning with the innermost set, in the order of 2, 3, and 4 below.
- Perform all exponential and root operations, moving left to right.
- Perform all multiplications and division, moving left to right.
- Perform all additions and subtractions, moving left to right.
One number as the factor of another (
[link] )
A first number is a factor of a second number if the first number divides into the second number a whole number of times.
Prime number (
[link] )
A whole number greater than one whose only factors are itself and 1 is called a
prime number . The whole number 1 is not a prime number. The whole number 2 is the first prime number and the only even prime number.
Composite number (
[link] )
A whole number greater than one that is composed of factors other than itself and 1 is called a
composite number .
Fundamental principle of arithmetic (
[link] )
Except for the order of factors, every whole number other than 1 can be written in one and only one way as a product of prime numbers.
Prime factorization (
[link] )
The prime factorization of 45 is
. The numbers that occur in this factorization of 45 are each prime.
Determining the prime factorization of a whole number (
[link] )
There is a simple method, based on division by prime numbers, that produces the prime factorization of a whole number. For example, we determine the prime factorization of 132 as follows.
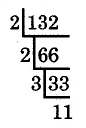
The prime factorization of 132 is
.
Common factor (
[link] )
A factor that occurs in each number of a group of numbers is called a
common factor . 3 is a common factor to the group 18, 6, and 45
Greatest common factor (gcf) (
[link] )
The largest common factor of a group of whole numbers is called the
greatest common factor . For example, to find the greatest common factor of 12 and 20,
- Write the prime factorization of each number.
- Write each base that is common to each of the numbers:
2 and 3
- The smallest exponent appearing on 2 is 2.
The smallest exponent appearing on 3 is 1.
- The GCF of 12 and 60 is the product of the numbers
and
.
Thus, 12 is the largest number that divides both 12 and 60 without a remainder.
Finding the gcf (
[link] )
There is a simple method, based on prime factorization, that determines the GCF of a group of whole numbers.
Multiple (
[link] )
When a whole number is multiplied by all other whole numbers, with the exception of zero, the resulting individual products are called
multiples of that whole number. Some multiples of 7 are 7, 14, 21, and 28.
Common multiples (
[link] )
Multiples that are common to a group of whole numbers are called
common multiples . Some common multiples of 6 and 9 are 18, 36, and 54.
The
least common multiple (LCM) of a group of whole numbers is the smallest whole number that each of the given whole numbers divides into without a remainder. The least common multiple of 9 and 6 is 18.
Finding the lcm (
[link] )
There is a simple method, based on prime factorization, that determines the LCM of a group of whole numbers. For example, the least common multiple of 28 and 72 is found in the following way.
- Write the prime factorization of each number
- Write each base that appears in each of the prime factorizations, 2, 3, and 7.
- To each of the bases listed in step 2, attach the
largest exponent that appears on it in the prime factorization.
,
, and
- The LCM is the product of the numbers found in step 3.
Thus, 504 is the smallest number that both 28 and 72 will divide into without a remainder.
The difference between the gcf and the lcm (
[link] )
The GCF of two or more whole numbers is the largest number that divides into each of the given whole numbers. The LCM of two or more whole numbers is the smallest whole number that each of the given numbers divides into without a remainder.
Source:
OpenStax, Fundamentals of mathematics. OpenStax CNX. Aug 18, 2010 Download for free at http://cnx.org/content/col10615/1.4
Google Play and the Google Play logo are trademarks of Google Inc.