3.6 Frequency transformations  (Page 2/2)

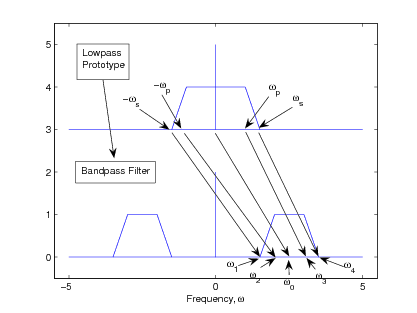
In order that the transformation give $-{\omega }_p=({\omega }_2^2-{\omega }_0^2)/{\omega }_2$ and ${\omega }_p=({\omega }_3^2-{\omega }_0^2)/{\omega }_3$ , the “center" frequency ${\omega }_0$ must be

However, because $-{\omega }_s=({\omega }_1^2-{\omega }_0^2)/{\omega }_1$ and ${\omega }_s=({\omega }_4^2-{\omega }_0^2)/{\omega }_4$ , the center frequency must also be

This means that only three of the four bandedge frequencies ${\omega }_1$ , ${\omega }_2$ , ${\omega }_3$ , and ${\omega }_4$ can be independently specified. Normally, ${\omega }_0$ is determined by ${\omega }_2$ and ${\omega }_3$ which then specifies the prototype passband edge by

and, using the same ${\omega }_0$ , the stopband edge is set by either ${\omega }_1$ or ${\omega }_4$ , whichever gives the smaller ${\omega }_s$ .

The finally designed bandpass filter will meet both passband edges and one transition band width, but the other will benarrower than originally specified. This is not a problem with the Butterworth or either of the Chebyshev approximation becausethey only have passband edges or stopband edges, but not both. The elliptic-function has both.

After the bandedges for the prototype lowpass filter ${\omega }_p$ and/or ${\omega }_s$ are calculated, the filter is designed by one of the optimal approximation methods discussed in this section or anyother means. Because most of these methods give the pole and zero locations directly, they can be individually transformed to givethe bandpass filter transfer function in factored form. This is accomplished by solving $s^2-ps+{\omega }_0^2$ from the original transformation to give for the root locations

This gives two transformed roots for each prototype root which doubles the order as expected.

The roots that result from transforming the real pole of an odd- order prototype cause some complication in programming thisprocedure. Program 8 should be studied to understand how this is carried out.

The band-reject filter

To design a filter that will reject a band of frequencies, a frequency transformation of the form

is used on the prototype lowpass filter. This transforms the origin of the $p$ -plane into both the origin and infinity of the $s$ -plane. It maps infinity in the $p$ -plane into j ${\omega }_0$ in the $s$ -plane.

Similar to the bandpass case, the transformation must give $-{\omega }_p={\omega }_4/({\omega }_0^2-{\omega }_4^2)$ and ${\omega }_p={\omega }_1/({\omega }_0^2-{\omega }_1^2)$ . A similar relationof ${\omega }_s$ to ${\omega }_2$ and ${\omega }_3$ requires that the center frequency ${\omega }_0$ must be

As before, only three of the four bandedge frequencies can be independently specified. Normally, ${\omega }_0$ is determined by ${\omega }_1$ and ${\omega }_4$ which then specifies the prototype passband edge by

and, using the same ${\omega }_0$ , the stopband edge is set by either ${\omega }_2$ or ${\omega }_3$ , whichever gives the smaller ${\omega }_s$ .

The finally designed bandpass filter will meet both passband edges and one transition-band width, but the other will benarrower than originally specified. This does not occur with the Butterworth or either Chebyshev approximation, only with theelliptic-function.

After the bandedges for the prototype lowpass filter ${\omega }_p$ and/or ${\omega }_s$ are calculated, the filter is designed. The poles and zeros of this filter are individually transformed to give thebandreject filter transfer function in factored form. This is carried out by solving $s^2-(1/p)s+{\omega }_0^2$ to give for the root locations

A more complicated set of transformations could be developed by using a general map of $s=f\left(s\right)$ with a higher order. Several pass or stopbands could be specified, but the calculations becomefairly complicated.

Although this method of transformation is a powerful and simple way for designing bandpass and bandreject filters, itdoes impose certain restrictions. A Chebyshev bandpass filter will be equal-ripple in the passband and maximally flat at bothzero and infinity, but the transformation forces the degree of flatness at zero and infinity to be equal. The elliptic-functionbandpass filter will bave the same number of ripples in both stopbands even if they are of very different widths. Theserestrictions are usually considered mild when compared with the complexity of alternative design methods.