| << Chapter < Page | Chapter >> Page > |
When you rise from lounging in a warm bath, your arms feel strangely heavy. This is because you no longer have the buoyant support of the water. Where does this buoyant force come from? Why is it that some things float and others do not? Do objects that sink get any support at all from the fluid? Is your body buoyed by the atmosphere, or are only helium balloons affected? (See [link] .)

Answers to all these questions, and many others, are based on the fact that pressure increases with depth in a fluid. This means that the upward force on the bottom of an object in a fluid is greater than the downward force on the top of the object. There is a net upward, or buoyant force on any object in any fluid. (See [link] .) If the buoyant force is greater than the object’s weight, the object will rise to the surface and float. If the buoyant force is less than the object’s weight, the object will sink. If the buoyant force equals the object’s weight, the object will remain suspended at that depth. The buoyant force is always present whether the object floats, sinks, or is suspended in a fluid.
The buoyant force is the net upward force on any object in any fluid.
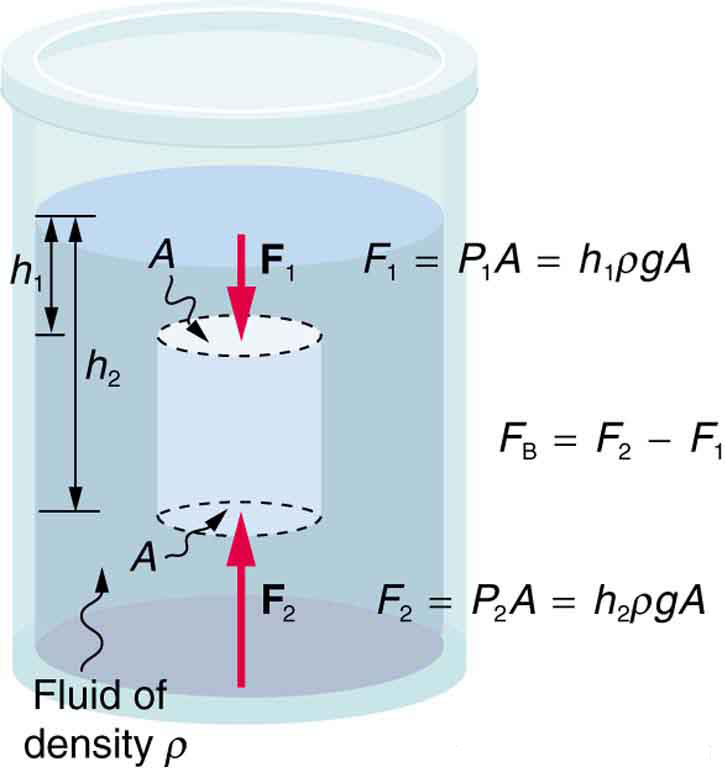
Just how great is this buoyant force? To answer this question, think about what happens when a submerged object is removed from a fluid, as in [link] .
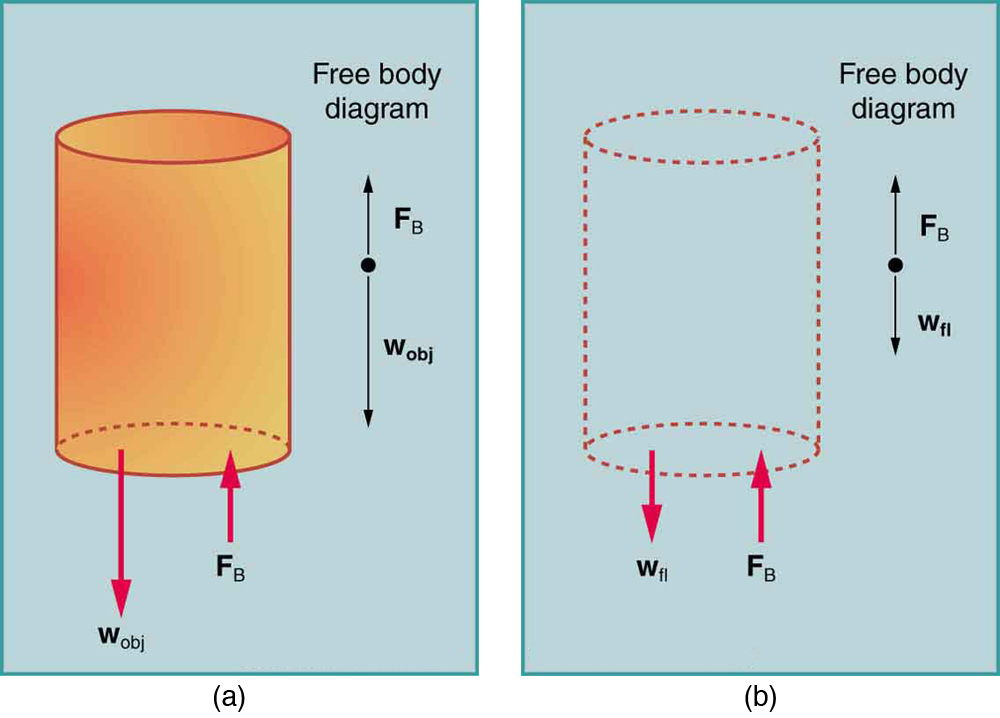
The space it occupied is filled by fluid having a weight . This weight is supported by the surrounding fluid, and so the buoyant force must equal , the weight of the fluid displaced by the object. It is a tribute to the genius of the Greek mathematician and inventor Archimedes (ca. 287–212 B.C.) that he stated this principle long before concepts of force were well established. Stated in words, Archimedes’ principle is as follows: The buoyant force on an object equals the weight of the fluid it displaces. In equation form, Archimedes’ principle is

Notification Switch
Would you like to follow the 'Physics 110 at une' conversation and receive update notifications?