| << Chapter < Page | Chapter >> Page > |
When a whole number is multiplied by other whole numbers, with the exception of zero, the resulting products are called multiples of the given whole number. Note that any whole number is a multiple of itself.
| Multiples of 2 | Multiples of 3 | Multiples of 8 | Multiples of 10 |
Find the first five multiples of the following numbers.
There will be times when we are given two or more whole numbers and we will need to know if there are any multiples that are common to each of them. If there are, we will need to know what they are. For example, some of the multiples that are common to 2 and 3 are 6, 12, and 18.
We can visualize common multiples using the number line.
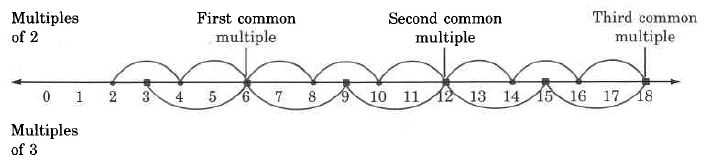
Notice that the common multiples can be divided by both whole numbers.
Find the first five common multiples of the following numbers.
Notice that in our number line visualization of common multiples (above), the first common multiple is also the smallest, or least common multiple , abbreviated by LCM .
The least common multiple will be extremely useful in working with fractions ( [link] ).
There are some major differences between using the processes for obtaining the GCF and the LCM that we must note carefully:
Find the LCM of the following numbers.
9 and 12
from 12.
from 9.
LCM
Thus, 36 is the smallest number that both 9 and 12 divide into without remainders.
90 and 630
LCM
Thus, 630 is the smallest number that both 90 and 630 divide into with no remainders.
33, 110, and 484
Thus, 7260 is the smallest number that 33, 110, and 484 divide into without remainders.
Find the LCM of the following numbers.
For the following problems, find the least common multiple of the numbers.
10 and 14
28 and 36
28 and 42
162 and 270
25 and 30
16 and 24
24 and 40
50 and 140
8, 10, and 15
4, 5, and 21
15, 25, and 40
84 and 96
12, 16, and 24
6, 9, 12, and 18
18, 80, 108, and 490
38, 92, 115, and 189
12, 12, and 12
( [link] ) Round 434,892 to the nearest ten thousand.
( [link] ) Find the quotient. .
( [link] ) Find the greatest common factor of 48 and 72.

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?