| << Chapter < Page | Chapter >> Page > |

A band marches down the field creating an amazing sound that bolsters the crowd. That sound travels as a wave that can be interpreted using trigonometric functions. For example, [link] represents a sound wave for the musical note A. In this section, we will investigate trigonometric identities that are the foundation of everyday phenomena such as sound waves.
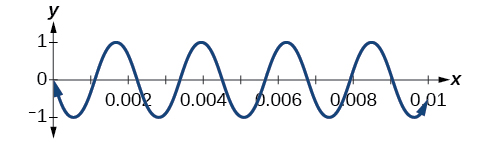
We have already learned a number of formulas useful for expanding or simplifying trigonometric expressions, but sometimes we may need to express the product of cosine and sine as a sum. We can use the product-to-sum formulas , which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity.
We can derive the product-to-sum formula from the sum and difference identities for cosine . If we add the two equations, we get:
Then, we divide by to isolate the product of cosines:
Given a product of cosines, express as a sum.
Write the following product of cosines as a sum:
We begin by writing the formula for the product of cosines:
We can then substitute the given angles into the formula and simplify.
Use the product-to-sum formula to write the product as a sum or difference:
Next, we will derive the product-to-sum formula for sine and cosine from the sum and difference formulas for sine . If we add the sum and difference identities, we get:
Then, we divide by 2 to isolate the product of cosine and sine:
Express the following product as a sum containing only sine or cosine and no products:
Write the formula for the product of sine and cosine. Then substitute the given values into the formula and simplify.
Use the product-to-sum formula to write the product as a sum:

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?