3.4 Special cases

Consider the two equations:

Suppose we attempt to solve these two equations by elimination. So, we double the first equation and subtract, and the result is:

Hey, what happened? 0 does not equal 13, no matter what $x$ is. Mathematically, we see that these two equations have no simultaneous solution. You asked the question “When will both of these equations be true?” And the math answered, “Hey, buddy, not until 0 equals 13.”

No solution .

Now, consider these equations:

Once again, we attempt elimination, but the result is different:

What happened that time? $0=0$ no matter what $x$ is. Instead of an equation that is always false, we have an equation that is always true. Does that mean these equations work for any $x$ and $y$ ? Clearly not: for instance, $(\mathrm{1,1})$ does not make either equation true. What this means is that the two equations are the same: any pair that solves one will also solve the other. There is an infinite number of solutions.

Infinite number of solutions .

All of this is much easier to understand graphically! Remember that one way to solve simultaneous equations is by graphing them and looking for the intersection. In the first case, we see that original equations represented two parallel lines . There is no point of intersection, so there is no simultaneous equation.

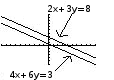
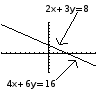
In the second case, we see that the original equations represented the same line, in two different forms . Any point on the line is a solution to both equations.