| << Chapter < Page | Chapter >> Page > |
Find the volume of the solid of revolution obtained by revolving the region enclosed by the graph of and the x -axis over the interval about the y -axis.
Let’s begin by sketching the region to be revolved (see [link] ). From the sketch, we see that the shell method is a good choice for solving this problem.
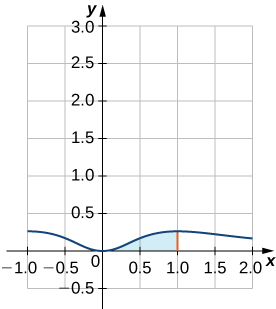
The volume is given by
Since we can proceed with partial fraction decomposition. Note that is a repeated irreducible quadratic. Using the decomposition described in the problem-solving strategy, we get
Finding a common denominator and equating the numerators gives
Solving, we obtain and Substituting back into the integral, we have
Express the rational function as a sum or difference of two simpler rational expressions.
( Hint: Use long division first.)
Use the method of partial fractions to evaluate each of the following integrals.
Evaluate the following integrals, which have irreducible quadratic factors.
Use the method of partial fractions to evaluate the following integrals.
Use substitution to convert the integrals to integrals of rational functions. Then use partial fractions to evaluate the integrals.
(Give the exact answer and the decimal equivalent. Round to five decimal places.)
Use the given substitution to convert the integral to an integral of a rational function, then evaluate.
Graph the curve over the interval Then, find the area of the region bounded by the curve, the x -axis, and the line
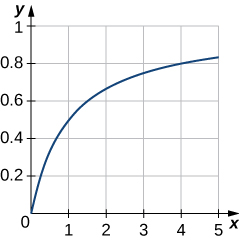
Find the volume of the solid generated when the region bounded by and is revolved about the x- axis.
The velocity of a particle moving along a line is a function of time given by Find the distance that the particle has traveled after sec.
Solve the initial-value problem for x as a function of t.
Find the x -coordinate of the centroid of the area bounded by
(Round the answer to two decimal places.)
Find the volume generated by revolving the area bounded by about the y -axis.
Find the area bounded by (Round the answer to the nearest hundredth.)
For the following problems, use the substitutions and
Find the area under the curve between and (Assume the dimensions are in inches.)
2.0 in. 2
Given derive the formulas and

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?