| << Chapter < Page | Chapter >> Page > |
We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them.
Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical. However, a particle traveling along a helix moves on a curve in three dimensions.
Let be a twice-differentiable vector-valued function of the parameter t that represents the position of an object as a function of time. The velocity vector of the object is given by
The acceleration vector is defined to be
The speed is defined to be
Since can be in either two or three dimensions, these vector-valued functions can have either two or three components. In two dimensions, we define and in three dimensions Then the velocity, acceleration, and speed can be written as shown in the following table.
| Quantity | Two Dimensions | Three Dimensions |
|---|---|---|
| Position | ||
| Velocity | ||
| Acceleration | ||
| Speed |
A particle moves in a parabolic path defined by the vector-valued function where t measures time in seconds.
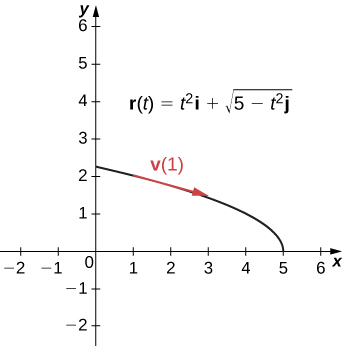
A particle moves in a path defined by the vector-valued function where t measures time in seconds and where distance is measured in feet. Find the velocity, acceleration, and speed as functions of time.
The units for velocity and speed are feet per second, and the units for acceleration are feet per second squared.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?