3.4 Analysing motion in a medium

The motion of an object body in a medium is composed of two motions : (i) motion of the object and (ii) motion of the medium. The resulting motion as observed by an observer in the reference frame is the resultant of two motions. The basic equation that governs the context of study is the equation of relative motion in two dimensions :

As discussed in the previous module, the motion of the body can alternatively be considered as the resultant of two motions. This concept of resultant motion is essentially an equivalent way of stating the concept of relative motion. Rearranging the equation, we have :

Both these equations are a vector equations, which can be broadly dealt in two ways (i) analytically (using graphics) and (ii) algebraically (using unit vectors). The use of a particular method depends on the inputs available and the context of motion.

Concept of independence of motion

Analysis of the motion of a body in a medium, specifically, makes use of independence of motions in two perpendicular directions. On a rectilinear coordinate system, the same principle can be stated in terms of component velocities. For example, let us consider the motion of a boat in a river, which tries to reach a point on the opposite bank of the river. The boat sails in the direction perpendicular to the direction of stream. Had the water been still, the boat would have reached the point exactly across the river with a velocity ( $v_y$ ). But, water body is not still. It has a velocity in x-direction. The boat, therefore, drifts in the direction of the motion of the water stream ( $v_x$ ).

Motion of a boat

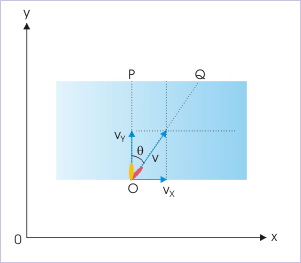
The important aspect of this motion is that the drift (x) depends on the component of velocity in x-direction. This drift (x) is independent of the component of velocity in y-direction. Why? Simply because, it is an experimental fact, which is fundamental to natural phenomena. We shall expand on this aspect while studying projectile motion also, where motions in vertical and horizontal directions are independent of each other.

In the case of boat, the displacements in the mutually perpendicular coordinate directions are :

Motion of boat in a stream

In this section, we shall consider a general situation of sailing of a boat in a moving stream of water. In order to keep our context simplified, we consider that stream is unidirectional in x-direction and the width of stream, “d”, is constant.

Let the velocities of boat (A) and stream (B) be “ ${\mathbf{v}}_A$ “ and “ ${\mathbf{v}}_B$ “ respectively with respect to ground. The velocity of boat (A) with respect to stream (B), therefore, is :

$${\mathbf{v}}_{AB}={\mathbf{v}}_A-{\mathbf{v}}_B$$

$$\Rightarrow {\mathbf{v}}_A={\mathbf{v}}_{AB}+{\mathbf{v}}_B$$

Resultant velocity

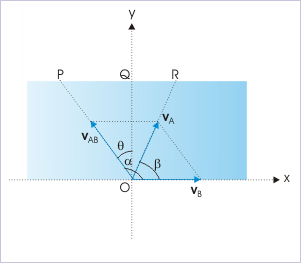
These velocities are drawn as shown in the figure. This is clear from the figure that boat sails in the direction, making an angle “θ” with y-direction, but reaches destination in different direction. The boat obviously is carried along in the stream in x-direction. The displacement in x-direction (x = QR) from the directly opposite position to actual position on the other side of the stream is called the drift of the boat.