3.3 Trigonometric substitution  (Page 8/5)

In this section, we explore integrals containing expressions of the form $\sqrt{a^2-x^2},$ $\sqrt{a^2+x^2},$ and $\sqrt{x^2-a^2},$ where the values of $a$ are positive. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution    comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as trigonometric integrals.

Integrals involving $\sqrt{a^2-x^2}$

Before developing a general strategy for integrals containing $\sqrt{a^2-x^2},$ consider the integral ${\displaystyle \int \sqrt{9-x^2}}dx.$ This integral cannot be evaluated using any of the techniques we have discussed so far. However, if we make the substitution $x=3\text{sin}\theta ,$ we have $dx=3\text{cos}\theta d\theta .$ After substituting into the integral, we have

After simplifying, we have

Letting $1-{\text{sin}}^2\theta ={\text{cos}}^2\theta ,$ we now have

Assuming that $\text{cos}\theta \ge 0,$ we have

At this point, we can evaluate the integral using the techniques developed for integrating powers and products of trigonometric functions. Before completing this example, let’s take a look at the general theory behind this idea.

To evaluate integrals involving $\sqrt{a^2-x^2},$ we make the substitution $x=a\text{sin}\theta$ and $dx=a\text{cos}\theta .$ To see that this actually makes sense, consider the following argument: The domain of $\sqrt{a^2-x^2}$ is $[\text{−}a,a].$ Thus, $\text{−}a\le x\le a.$ Consequently, $\mathrm{-1}\le \frac{x}{a}\le 1.$ Since the range of $\text{sin}x$ over $\left[\text{−}(\pi \text{/}2),\pi \text{/}2\right]$ is $[\mathrm{-1},1],$ there is a unique angle $\theta$ satisfying $\text{−}(\pi \text{/}2)\le \theta \le \pi \text{/}2$ so that $\text{sin}\theta =x\text{/}a,$ or equivalently, so that $x=a\text{sin}\theta .$ If we substitute $x=a\text{sin}\theta$ into $\sqrt{a^2-x^2},$ we get

Since $\text{cos}x\ge 0$ on $-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}$ and $a>0,$ $\left|a\text{cos}\theta \right|=a\text{cos}\theta .$ We can see, from this discussion, that by making the substitution $x=a\text{sin}\theta ,$ we are able to convert an integral involving a radical into an integral involving trigonometric functions. After we evaluate the integral, we can convert the solution back to an expression involving $x.$ To see how to do this, let’s begin by assuming that $0<x<a.$ In this case, $0<\theta <\frac{\pi }{2}.$ Since $\text{sin}\theta =\frac{x}{a},$ we can draw the reference triangle in [link] to assist in expressing the values of $\text{cos}\theta ,$ $\text{tan}\theta ,$ and the remaining trigonometric functions in terms of $x.$ It can be shown that this triangle actually produces the correct values of the trigonometric functions evaluated at $\theta$ for all $\theta$ satisfying $-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}.$ It is useful to observe that the expression $\sqrt{a^2-x^2}$ actually appears as the length of one side of the triangle. Last, should $\theta$ appear by itself, we use $\theta ={\text{sin}}^{\mathrm{-1}}\left(\frac{x}{a}\right).$

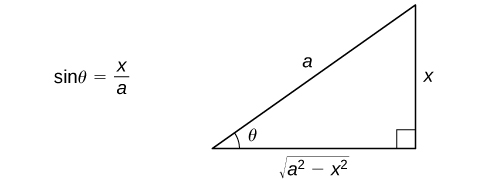
The essential part of this discussion is summarized in the following problem-solving strategy.