1. Home
  2. Mathematics grade 7
  3. Term 3
  4. More revision

3.3 More revision

<< Chapter < Page
  Mathematics grade 7   Page 1 / 1
Chapter >> Page >

Mathematics

Decimal fractions

Educator section

Memorandum

13.4

a) 2 60 100 size 12{ { { size 8{"60"} } over { size 8{"100"} } } } {} 2,60
b) 13 625 1000 size 12{ { { size 8{"625"} } over { size 8{"1000"} } } } {} 13,625
c) 17 75 100 size 12{ { { size 8{"75"} } over { size 8{"100"} } } } {} 17,75
d) 23 875 1000 size 12{ { { size 8{"875"} } over { size 8{"1000"} } } } {} 23,875
e) 36 8 10 size 12{ { { size 8{8} } over { size 8{"10"} } } } {} 36,8

13.5 a) 0,83

  1. 0,2857142
  2. 0,8125
  3. 0,4

13.6

9 2 size 12{ { { size 8{9} } over { size 8{2} } } } {} 11 2 size 12{ { { size 8{"11"} } over { size 8{2} } } } {} 325 100 size 12{ { { size 8{"325"} } over { size 8{"100"} } } } {} 43 5 size 12{ { { size 8{"43"} } over { size 8{5} } } } {} 201 8 size 12{ { { size 8{"201"} } over { size 8{8} } } } {} 4056 1000 size 12{ { { size 8{"4056"} } over { size 8{"1000"} } } } {} 199 5 size 12{ { { size 8{"199"} } over { size 8{5} } } } {}
4 1 2 size 12{ { { size 8{1} } over { size 8{2} } } } {} 5 1 2 size 12{ { { size 8{1} } over { size 8{2} } } } {} 3 25 100 size 12{ { { size 8{"25"} } over { size 8{"100"} } } } {} 8 3 5 size 12{ { { size 8{3} } over { size 8{5} } } } {} 25 1 8 size 12{ { { size 8{1} } over { size 8{8} } } } {} 4 56 1000 size 12{ { { size 8{"56"} } over { size 8{"1000"} } } } {} 39 4 5 size 12{ { { size 8{4} } over { size 8{5} } } } {}
4,5 5,5 3,25 8,6 25,125 4,056 39,8

14. a) 0,3

  1. 0,6
  2. 0,23

Leaner section

Content

Activity: more revision [lo 1.4.2, lo 1.10, lo 2.3.1, lo 2.3.3]

We can convert proper fractions to decimal fractions in this way:

13.2 Did you know?

We can also calculate it in this way:

13.3 Which of the methods shown above do you choose?

Why?

13.4 Complete the following tables:

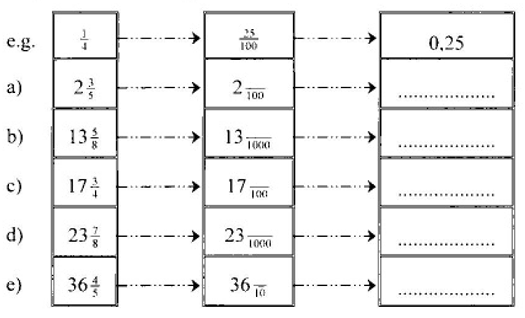
13.5 Use the division method as shown in 13.2 and write the following fractions as decimal fractions:

a) 5 6 size 12{ { {5} over {6} } } {} ........................................................................... ...........................................................................

...........................................................................

b) 2 7 size 12{ { {2} over {7} } } {} ........................................................................... ...........................................................................

...........................................................................

c) 13 16 size 12{ { {"13"} over {"16"} } } {} ........................................................................... ...........................................................................

...........................................................................

d) 4 9 size 12{ { {4} over {9} } } {} ........................................................................... ...........................................................................

...........................................................................

13.6 Can you complete the following table??

Improper fraction 9 2 size 12{ { { size 8{9} } over { size 8{2} } } } {} 45 5 size 12{ { { size 8{"45"} } over { size 8{5} } } } {}
Mixed Number 5 1 2 size 12{5 { { size 8{1} } over { size 8{2} } } } {} 25 1 8 size 12{"25" { { size 8{1} } over { size 8{8} } } } {} 39 4 5 size 12{"39" { { size 8{4} } over { size 8{5} } } } {}
Decimal fraction 3,25 4,056

14. BRAIN-TEASERS!

Write the following fractions as decimal fractions. Try to do these sums first without a calculator!

a) 1 3 size 12{ { {1} over {3} } } {} ........................................................................... ...........................................................................

...........................................................................

b) 2 3 size 12{ { {2} over {3} } } {} ........................................................................... ...........................................................................

...........................................................................

c) 23 99 size 12{ { {"23"} over {"99"} } } {} ........................................................................... ...........................................................................

...........................................................................

15. Do you still remember?

We call 0,666666666 . . . a recurring decimal . We write it as 0, 6 size 12{0, {6} cSup { size 8{ cdot } } } {} .

0,454545 . . . is also a recurring decimal and we write it as 0, 4 5 size 12{0, {4} cSup { size 8{ cdot } } {5} cSup { size 8{ cdot } } } {} .

We normally round off these recurring decimals to the first or second decimal place, e.g.: 0, 6 size 12{0, {6} cSup { size 8{ cdot } } } {} becomes 0,7 or 0,67 and 0, 4 5 size 12{0, {4} cSup { size 8{ cdot } } {5} cSup { size 8{ cdot } } } {} becomes 0,5 or 0,45

16. Time for self-assessment

  • Tick the applicable block:
 YES NO
I can:
Compare decimal fractions with each other and put them in the correct sequence.
Fill in the correct relationship signs.
Round off decimal fractions correctly to:
  • the nearest whole number
  • one decimal place
  • two decimal places
  • three decimal places
Convert fractions and improper fractions correctly to decimal fractions.
Explain what a recurring decimal is.

Assessment

Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.

Assessment Standard 1.4: We know this when the learner recognises and uses equivalent forms of the rational numbers listed above, including:

1.4.2 decimals;

Assessment Standard 1.10: We know this when the learner uses a range of strategies to check solutions and judges the reasonableness of solutions.

Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.

Assessment Standard 2.3: We know this when the learner represents and uses relationships between variables in a variety of ways using:

2.3.1 verbal descriptions;

2.3.3 tables.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Mathematics grade 7. OpenStax CNX. Sep 16, 2009 Download for free at http://cnx.org/content/col11075/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Mathematics grade 7' conversation and receive update notifications?

Ask