If
and
is in quadrant I.
If
and
is in quadrant III.
If
and
is in quadrant IV.
For the following exercises, find the values of the six trigonometric functions if the conditions provided hold.
and
and
For the following exercises, simplify to one trigonometric expression.
For the following exercises, find the exact value using half-angle formulas.
For the following exercises, find the exact values of a)
b)
and c)
without solving for
If
and
is in quadrant IV.
If
and
is in quadrant III.
a)
b)
c)
If
and
is in quadrant II.
If
and
is in quadrant II.
For the following exercises, use
[link] to find the requested half and double angles.
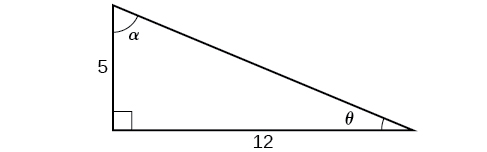
Find
and
Find
and
Find
and
Find
and
For the following exercises, simplify each expression. Do not evaluate.
For the following exercises, prove the identity given.
For the following exercises, rewrite the expression with an exponent no higher than 1.
Technology
For the following exercises, reduce the equations to powers of one, and then check the answer graphically.
For the following exercises, algebraically find an equivalent function, only in terms of
and/or
and then check the answer by graphing both equations.
Extensions
For the following exercises, prove the identities.

