| << Chapter < Page | Chapter >> Page > |
Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.

Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations
and
Step 2: Add the horizontal and vertical components of each vector to determine the components and of the resultant vector, :
and
Step 3: Use the Pythagorean theorem to determine the magnitude, , of the resultant vector :
Step 4: Use a trigonometric identity to determine the direction, , of :
Suppose you add two vectors and . What relative direction between them produces the resultant with the greatest magnitude? What is the maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?
Give an example of a nonzero vector that has a component of zero.
Explain why a vector cannot have a component greater than its own magnitude.
If the vectors and are perpendicular, what is the component of along the direction of ? What is the component of along the direction of ?
Find the following for path C in
[link] : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
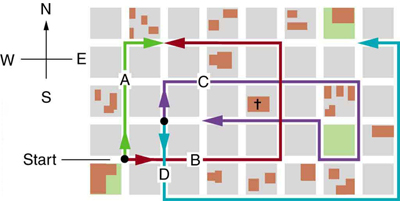
(a) 1.56 km
(b) 120 m east
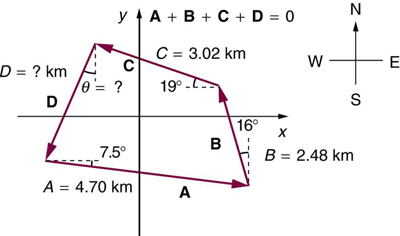
Find the following for path D in [link] : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
Find the north and east components of the displacement from San Francisco to Sacramento shown in
[link] .
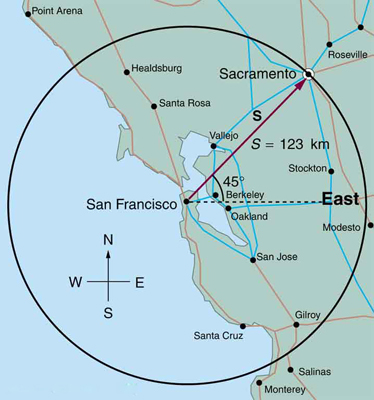
North-component 87.0 km, east-component 87.0 km
Solve the following problem using analytical techniques: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements and , as in [link] , then this problem asks you to find their sum .)
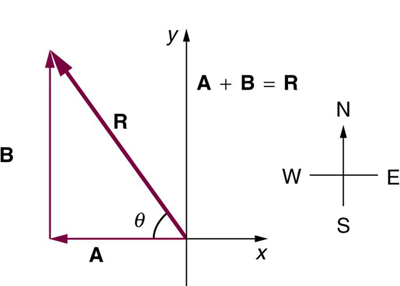
Note that you can also solve this graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.
Repeat [link] using analytical techniques, but reverse the order of the two legs of the walk and show that you get the same final result. (This problem shows that adding them in reverse order gives the same result—that is, .) Discuss how taking another path to reach the same point might help to overcome an obstacle blocking you other path.
30.8 m, 35.8 west of north
You drive in a straight line in a direction east of north. (a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.) (b) Show that you still arrive at the same point if the east and north legs are reversed in order.
Do [link] again using analytical techniques and change the second leg of the walk to straight south. (This is equivalent to subtracting from —that is, finding ) (b) Repeat again, but now you first walk north and then east. (This is equivalent to subtract from —that is, to find . Is that consistent with your result?)
(a) , south of west
(b) , north of east
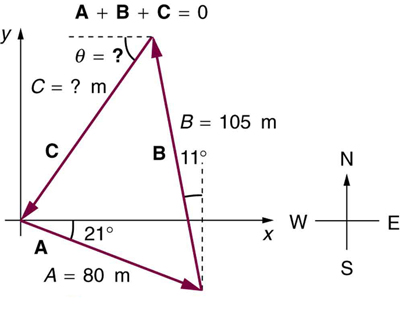
A new landowner has a triangular piece of flat land she wishes to fence. Starting at the west corner, she measures the first side to be 80.0 m long and the next to be 105 m. These sides are represented as displacement vectors
from
in
[link] . She then correctly calculates the length and orientation of the third side
. What is her result?
You fly in a straight line in still air in the direction south of west. (a) Find the distances you would have to fly straight south and then straight west to arrive at the same point. (This determination is equivalent to finding the components of the displacement along the south and west directions.) (b) Find the distances you would have to fly first in a direction south of west and then in a direction west of north. These are the components of the displacement along a different set of axes—one rotated .
18.4 km south, then 26.2 km west(b) 31.5 km at south of west, then 5.56 km at west of north
A farmer wants to fence off his four-sided plot of flat land. He measures the first three sides, shown as and in [link] , and then correctly calculates the length and orientation of the fourth side . What is his result?
In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines: north of west; then south of east; then south of west; then straight east; then east of north; then south of west; and finally north of east. What is his final position relative to the island?
, south of east
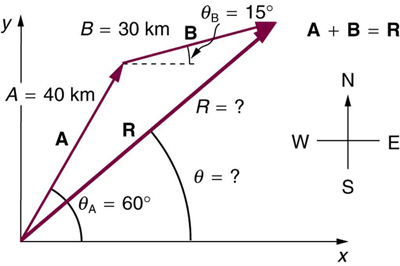
Suppose a pilot flies in a direction north of east and then flies in a direction north of east as shown in [link] . Find her total distance from the starting point and the direction of the straight-line path to the final position. Discuss qualitatively how this flight would be altered by a wind from the north and how the effect of the wind would depend on both wind speed and the speed of the plane relative to the air mass.

Notification Switch
Would you like to follow the 'Cc test coll' conversation and receive update notifications?