3.15 Composition of trigonometric function and its inverse  (Page 42/3)

Trigonometric and inverse trigonometric functions are inverse to each other. We can use them to compose new functions. In such composition, trigonometric function represents value of trigonometric ratio, whereas inverse trigonometric function represents angle. The composite function either evaluates to value or angle, depending on particular composition.

Composition representing value of trigonometric function

Sine inverse trigonometric function is given by :

$$y={\sin }^{-1}x\Rightarrow x=\sin y\Rightarrow x=\sin {\sin }^{-1}x$$

$$\Rightarrow \sin {\sin }^{-1}x=x$$

The composition $\sin {\sin }^{-1}x$ evaluates to a value. Clearly, x is a value of sine trigonometric function which falls within the range of sine function i.e $x\in [-\mathrm{1,1}]$ . It is important to note that domain of inverse function is same as range of the corresponding trigonometric function. We write six compositions denoting value of trigonometric functions as :

$$\sin {\sin }^{-1}x=x;x\in [-\mathrm{1,1}]$$

$$\cos {\cos }^{-1}x=x;x\in [-\mathrm{1,1}]$$

$$\tan {\tan }^{-1}x=x;x\in R$$

$$\cot {\cot }^{-1}x=x;x\in R$$

$$\sec {\sec }^{-1}x=x;x\in \left(-\infty ,-1]\cup [\mathrm{1,}\infty \right)$$

$$\mathrm{cosec}{\mathrm{cosec}}^{-1}x=x;x\in \left(-\infty ,-1]\cup [\mathrm{1,}\infty \right)$$

Composition representing angle

We shall discuss this composition with respect to individual inverse trigonometric ratio.

Composition with arcsine

Sine inverse trigonometric function is given by :

$$y={\sin }^{-1}x\Rightarrow x=\sin y\Rightarrow y={\sin }^{-1}\sin y$$

In order to maintain generality, we replace y by x as :

$$\Rightarrow {\sin }^{-1}\sin x=x$$

The composition ${\sin }^{-1}\sin x$ evaluates to an angle. Clearly, x is angle value – not the value of trigonometric ratio. However, we know that we use a truncated domain of trigonometric function for defining range of inverse function. The values in the interval are selected such that all unique values of sine trigonometric function are represented. It means that expression on LHS of the equation i.e. ${\sin }^{-1}\sin x$ evaluates to angle values lying in the interval $[-\pi /\mathrm{2,}\pi /2]$ .

$${\sin }^{-1}\sin x=x;x\in [-\frac{\pi }{2},\frac{\pi }{2}]$$

However, x as argument of sine function can assume angle values belonging to real number set. It means angles represented by LHS and RHS can be different if we consider angle values beyond principal set selected to render corresponding trigonometric function invertible.

Sine function

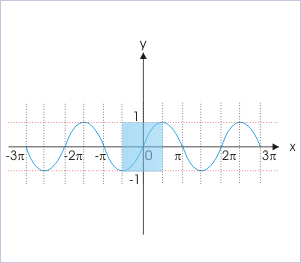
Let us consider adjacent intervals such that all sine values are included once. Such intervals are $[\pi /\mathrm{2,}3\pi /2],[3\pi /\mathrm{2,}5\pi /2]$ etc on the right side and $[-3\pi /\mathrm{2,}-\pi /2],[-5\pi /\mathrm{2,}-3\pi /2]$ etc on the left side of the principal interval.

Sine function

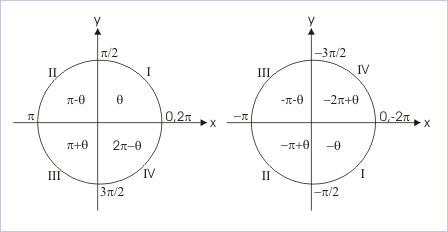
Our task now is to determine angles in any of these new intervals, say $[\pi /\mathrm{2,}3\pi /2]$ , corresponding to angles in the principal interval. We make use of value diagram which allows to determine angles having same trigonometric values. Let us consider a positive acute angle “θ” in the principal interval. This lies in the first quadrant. The new interval represents second and third quadrants. However, sine is positive in second quadrant and negative in third quadrant. Let the angle corresponding to positive acute angle in principal interval be x. Clearly, x corresponding to positive acute angle θ lies in second quadrant and is given by :

Value diagrams