| << Chapter < Page | Chapter >> Page > |
The abrupt change in the refractive index or the dielectric constant is referred to as step index change. In the same way abrupt voltage change is referred to as step voltage change.
Matter wave behaves in an analogous fashion at a step voltage change as a light wave behaves at step index change.
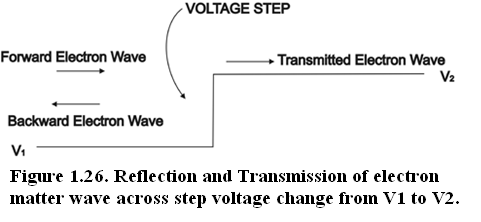
Fig(1.26) Reflection and Transmission of electron matter wave across step voltage change from V 1 to V 2 .
For matter wave,
wave vector k=2π/λ = 2πp/h = [√{2m(E-V)}]/ћ;
Therefore the two wave vectors are:
k 1 = [√{2m(E-V 1 )}]/ћ and k 2 = [√{2m(E-V 2 )}]/ћ;
The incident forward electron matter wave:
ψ(z,t) incident = ψ 0incident Exp[j(ωt- k z1 .z)]
The reflected backward electron wave:
ψ(z,t) reflected = ψ 0reflected Exp[j(ωt+ k z1 .z)] 1.55
The transmitted forward electron wave:
ψ(z,t) transmitted = ψ 0transmitted Exp[j(ωt- k z2 .z)] 1.56
At the interface or at the step,
ψ 0incident - ψ 0reflected = ψ 0transmitted 1.57
Eq.(1.57) is the interface boundary condition.
Now we return to the original infinite potential well case.
Inside the potential well we have both the wave vectors ±i[√{2mE}]/ћ]hence we have both forward and backward traveling wave components.
Outside the well Schrodinger Equation is of the form:
∂ 2 ψ /∂x 2 + (2m(E-V)/ћ 2 )ψ = 0
But outside the well, V = ∞ therefore the wave equation reduces to:
∂ 2 ψ /∂x 2 - (2m∞/ћ 2 )ψ = 0
The characteristic equation has real roots hence the solution is hyperbolic.
Therefore ψ(z,t) = [AExp(-k 2 .z) + BExp(+k 2 .z)]Exp(iωt) 1.58
Where k 2 = [√{2m∞}]/ћ]
In Eq(1.58), the term Exp(+k 2 .z) is not admissible as it is exponentially growing function. Hence B=0 and the solution outside the well is:
ψ(z,t) = [AExp(-k 2 .z)]Exp(iωt) 1.59
But since k 2 = infinity implies the wave function does not exist outside the well. The transmitted wave outside the well almost instantaneously attenuates to zero since k 2 is the attenuation coefficient of the exponentially decaying wave and this coefficient is infinite.
Inside the potential well there are two waves one forward and the second backward and both have equal amplitude but opposite sign so that at the two boundaries of the potential well the sum of the two produce nodes.
ψ 0incident - ψ 0reflected = 0 at the boundaries 1.60
Therefore
ψ(z,t) incident = A Exp[j(ωt- k z1 .z)]
ψ(z,t) reflected = -AExp[j(ωt+ k z1 .z)] 1.61
The superposition of the two waves is:
ψ(z,t) = AExp[j(ωt)] [ Exp(- k z1 .z)- Exp(+ k z1 .z)]
ψ(z,t) = AExp[j(ωt)][Cos(k z1 .z)-iSin(k z1 .z) -Cos(k z1 .z)-iSin(k z1 .z)]
ψ(z,t) = -2iAExp[j(ωt)][Sin(k z1 .z)]
or ψ(z,t) = BExp[j(ωt)][Sin(k z1 .z)] 1.62
Eq.(1.62) is the mathematical formulation of the standing wave.
According to boundary conditions, this standing wave is suppose to have two nodes :
ψ(0,t)= ψ(W,t) =0
therefore k z1 .W = (2π/λ n )W = n π where n = 1, 2, 3,………….
Therefore W=n. λ n /2 1.63
This is the same restriction as was imposed in Eq.(1.51). This Eq(1.63) sheds a very important light on the quantization of energy levels permitted for an electron in an infinite potential well.
Inside the potential well there is the superposition of incident and reflected wave. There are only certain cases for which constructive interference takes place for the remaining cases there is destructive interference.
The cases for which the superposition leads to node formation at the boundaries z = 0 and W, only for those cases electron has an existence. For all the remaining cases electron goes out of existence by destructive interference.
Therefore we assert that in an infinite potential well , the electron can be in existence only for the energy levels:
E= E 0 , 4 E 0 , 9 E 0 , 16 E 0 ………
Where E 0 = h 2 /(8mW 2 )
The above result comes from Eq.(1.50) and its previous line.
An identical situation prevails in a hydrogen atom. The orbits which allow constructive interference to take place only those orbits are permitted. Remaining are forbidden. The orbital radii which support constructive interference are the radii where electron can exist as standing wave.
These are the radii exactly predicted by Bohr’s Law:
Orbital Angular Momentum = Integral Multiple of (h/(2π)) as already seen in Chapter 1_part 6.
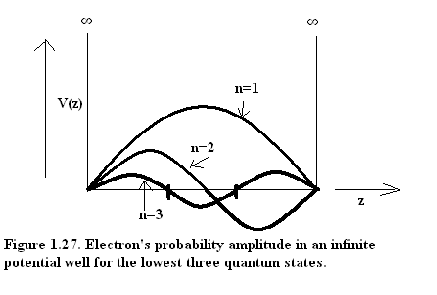
Fig(1.27) An electron in 3 quantum states n=1,2,3 in an infinite potential well.
An electron in first three permissible quantum states in an infinite potential well are shown in Fig.(1.27

Notification Switch
Would you like to follow the 'Solid state physics and devices-the harbinger of third wave of civilization' conversation and receive update notifications?