| << Chapter < Page | Chapter >> Page > |
We are familiar with trigonometric ratios, identities and their applications. In this module, we shall revisit the concept of trigonometric ratios from the perspective of a function. For this, we shall first recapitulate a bit of basics and important results and then emphasize: how can we conceive trigonometric ratio as a function?
The most important aspect, here, is the extension of the concept of angle beyond the domain of 2π i.e. the angle of "1" revolution. This concept is followed by the investigation of trigonometric ratios, which is originally defined for acute angle. Here, we shall apply these ratios in the context of any real value angle, represented on a real number line.
The measurement of angle is constrained to a circular periphery. We can unwind this constraint and think of angle as a real number, extending from minus infinity to plus infinity. For this, we imagine the circular periphery straightened into a line. Alternatively, we may think angle be represented along a straight line like real number and then think to bend straight line along the periphery of the circle. Following this visualization, we consider angle as if it were represented by a real number line, which is tangent to the circle.
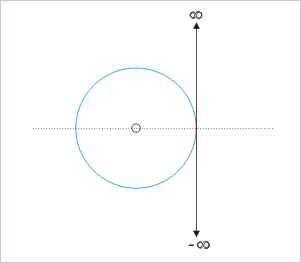
The positive section of the real number line can be wrapped many times over in the anticlockwise direction. Similarly, the negative section of the number line can be wrapped many times over in the clockwise direction.
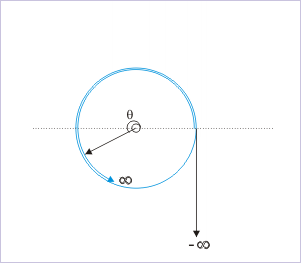
We consider representation of angle on real number line equivalent to measurement of angle from a reference direction about the central vertex “O” in as many revolutions as required. The measurement of angle in anticlockwise direction is considered positive and negative in clockwise direction.
Trigonometric ratios are defined for acute angle in a right angle triangle. Even for angles, which are not acute, we consider trigonometric ratios as ratios of sides or ratios of a side and hypotenuse of the right angle triangle OAB, which is constructed with the terminal ray, “OA” (measuring angle from the initial position in x-direction) and x-axis. The cosine of angle “θ”, in terms of side and hypotenuse of triangle OAB, is :
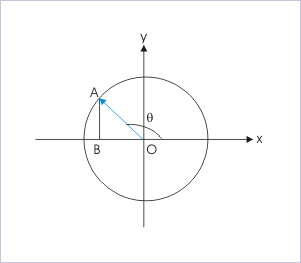
cosθ=OBOA
Clearly, the sign of ratio is given by the sign of the side of the right angle triangle OAB, involved in the ratio. We attach sign to bidirectional measurements along x and y axes. We can not attach sign to the radial ray OA as it can be directed in multiple directions. In the case shown above, side of the triangle “OB” is negative with respect to positive x-direction. As such, the cosine of “θ” in this particular case is negative. However, note that “AB” is positive and hence sine of the angle, which involves “AB”, is positive for the same angle.
sinθ=ABOA
Alternatively, the sign of “x” and “y” coordinates of the final ray on the circle decides the sign of trigonometric ratio. As one of the coordinates is involved in the ratio, its sign becomes the sign of trigonometric ratio. Consider the position, “A”, shown in the figure.

Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?