| << Chapter < Page | Chapter >> Page > |
TEGNOLOGIE
Graad 9
HIDROULIESE EN PNEUMATIESE STELSELS
Module 11
Om die meganiese voordeel van ’n hidrouliese stelsel te bereken
Aktiwiteit 1:
Om die meganiese voordeel van ’n hidrouliese stelsel te bereken
[LU 2.3]
’n Voorbeeld van ’n eenvoudige hidrouliese stelsel is ’n hidrouliese hyser om motors mee op te lig. Die stelsel het ’n meganiese voordeel van beide kraglewering en afstandlewering.
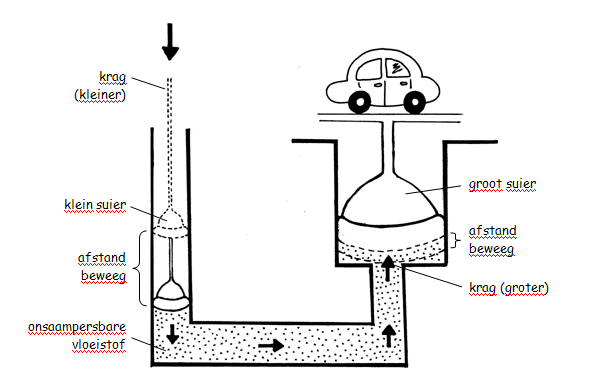
Die stelsel bestaan uit twee suiers van verskillende groottes verbind met ’n reservoir, gevul met ’n hidrouliese vloeistof soos olie of water.
Meganiese voordeel – kraglewering:
’n Klein insetkrag op die klein suier veroorsaak altyd ’n groot uitsetkrag op die groot suier sodat daar ’n meganiese voordeel is.
Die insetkrag word die mag genoem en die uitsetkrag die las.
Die voordeel word moontlik gemaak deur die eienskap van ’n vloeistof dat dit nie saamgepers kan word nie en druk eweredig versprei.
Hierdie beginsel staan bekend as Pascal se beginsel.
Die druk by suier A is gelyk aan die druk by suier B.
Druk word bereken as krag per oppervlakte.
Om die meganiese voordeel te bereken, kan jy die volgende formule gebruik:
Meganiese voordeel – afstandlewering:
In die spuite sal die suier met die groot deursnee, ’n klein afstandlewering hê en die suier met die klein deursnee, ’n groot afstandlewering. Die verhouding van afstandlewering word bepaal deur die meganiese kragvoordeel.
Voorbeeld:
Die motor in bogenoemde voorbeeld het ’n gewig van 5000 N. Die klein suier, A het ’n oppervlak van 1 cm2 en die groot suier, B het ’n oppervlak van 100 cm2. Die klein suier beweeg oor ’n afstand van 100 cm.
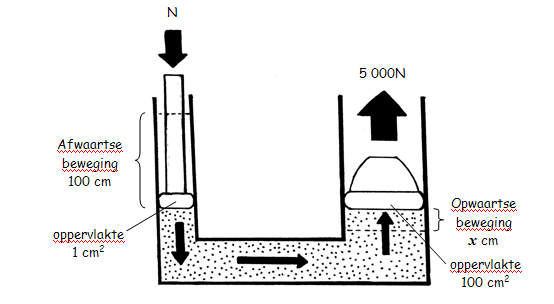
(a) Bepaal die insetkrag (mag). Volgens Pascal se beginsel sal:
Die oppervlak by silinder B is 100 x kleiner. Daarom is die krag by silinder A 100 keer kleiner.
(b) Bepaal die meganiese kragvoordeel.
(c) Bepaal die afstand wat die groot suier gaan beweeg.
MA= 100. As die klein suier dus 100 cm beweeg, sal die groot suier 1 cm beweeg.
Toets Jou Kennis
’n Klein seuntjie kry ’n Kisduiweltjie (Jack-in-the-box), soos in die skets aangedui, by sy ouma.
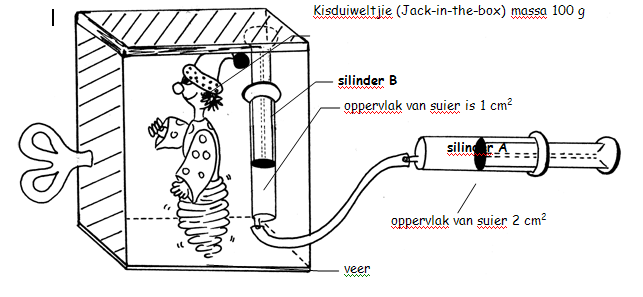
1.1 Bereken die hoeveelheid krag, in newton, wat die seuntjie benodig om die Kisduiweltjie (Jack-in-the-box) van 100 g te laat uitskiet, wanneer die oppervlak by silinder A, 2 cm2 is en die oppervlak by silinder B, 1 cm2 is.
1.2 Bereken die meganiese voordeel in vraag 1.1
1.3 Bereken die afstand wat silinder A moet beweeg om die Kisduiweltjie (Jack-in-the-box) 3 cm te laat uitskiet.
1.4 Sou dit meer voordelig wees om die twee suiers, A en B, om te ruil?
Jy moet ’n hidrouliese tang maak, soos in die skets aangedui. Om die opdrag uit te voer, ontvang jy twee silinders met suiers van 2 cm en 1 cm deursnee, onderskeidelik. Die maksimum afstand wat die groter suier in die silinder kan beweeg is 3 cm. ’n Krag van 1 N word aangewend om die bewegende kaak van die tang oor ’n afstand van 3 cm te beweeg en sodoende die tang toe te knyp.
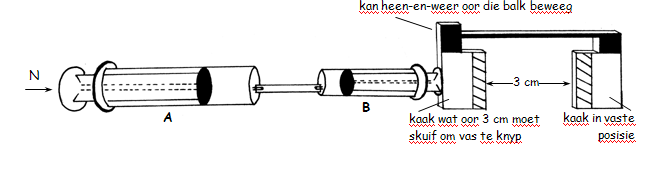
2.1 Watter een van die twee suiers gaan jy by posisie A, vir ’n minimum krag-inset plaas? Verduidelik jou antwoord.
2.2 Hoe ver sal die suier by silinder A beweeg?
Assessering
| LU 2 |
| Tegnologiese Kennis en BegripDie leerder is in staat om relevante tegnologiese kennis te verstaan en dit eties en verantwoordelik toe te pas. |
| Dit is duidelik wanneer die leerder: |
| stelsels en beheer:2.3 deur praktiese analise, kennis en begrip van interaktiewe meganiese sisteme en subsisteme demonstreer en sulke sisteme en subsisteme met diagrammatiese sisteemdiagramme voorstel: |
| ratstelsels; |
| bandaangedrewe of katrolstelsels met meer as een stadium; |
| pneumatiese of hidroliese stelsels wat beperkers gebruik; |
| eenrigtingkleppe; |
| stelsels waar meganiese, elektriese, pneumatiese of hidroliese stelsels gekombineer word. |
Memorandum
AKTIWITEIT 1
1.1 KRAG = 2 N
1.2 MA=1/2
1.3 1,5 cm
1.4 Nee, die klein suier sal die verste beweeg en Jack die hoogste laat spring.
2.1 Die suier met ‘n 1 cm-deursnee.
2.2 1,5 cm

Notification Switch
Would you like to follow the 'Tegnologie graad 9' conversation and receive update notifications?