1. Home
  2. Une: physics for the health
  3. Unit 03 - constant acceleration
  4. Motion equations for constant

3.1 Motion equations for constant acceleration in one dimension  (Page 7/8)

<< Chapter < Page
  Une: physics for the health     Page 7 / 8
Chapter >> Page >

A manned rocket accelerates at a rate of 20 m/s 2 size 12{"20 m/s" rSup { size 8{2} } } {} during launch. How long does it take the rocket to reach a velocity of 400 m/s?

To answer this, choose an equation that allows you to solve for time t size 12{t} {} , given only a size 12{a} {} , v 0 size 12{v rSub { size 8{0} } } {} , and v size 12{v} {} .

v = v 0 + at size 12{v=v"" lSub { size 8{0} } + ital "at"} {}

Rearrange to solve for t size 12{t} {} .

t = v − v 0 a = 400 m/s − 0 m/s 20 m/s 2 = 20 s size 12{t= { {v - v"" lSub { size 8{0} } } over {a} } = { {"400 m/s" - "0 m/s"} over {"20 m/s" rSup { size 8{2} } } } ="20 s"} {}

Section summary

  • To simplify calculations we take acceleration to be constant, so that a - = a size 12{ { bar {a}}=a} {} at all times.
  • We also take initial time to be zero.
  • Initial position and velocity are given a subscript 0; final values have no subscript. Thus,
    Δ t = t Δ x = x − x 0 Δ v = v − v 0
  • The following kinematic equations for motion with constant a size 12{a} {} are useful:
    x = x 0 + v - t size 12{x=x rSub { size 8{0} } + { bar {v}}t} {}
    v - = v 0 + v 2 size 12{ { bar {v}}= { {v rSub { size 8{0} } +v} over {2} } } {}
    v = v 0 + at size 12{v=v rSub { size 8{0} } + ital "at"} {}
    x = x 0 + v 0 t + 1 2 at 2 size 12{x=x rSub { size 8{0} } +v rSub { size 8{0} } t+ { {1} over {2} } ital "at" rSup { size 8{2} } } {}
    v 2 = v 0 2 + 2 a x − x 0 size 12{v rSup { size 8{2} } =v rSub { size 8{0} } rSup { size 8{2} } +2a left (x - x rSub { size 8{0} } right )} {}
  • In vertical motion, y size 12{y} {} is substituted for x size 12{x} {} .

Problems&Exercises

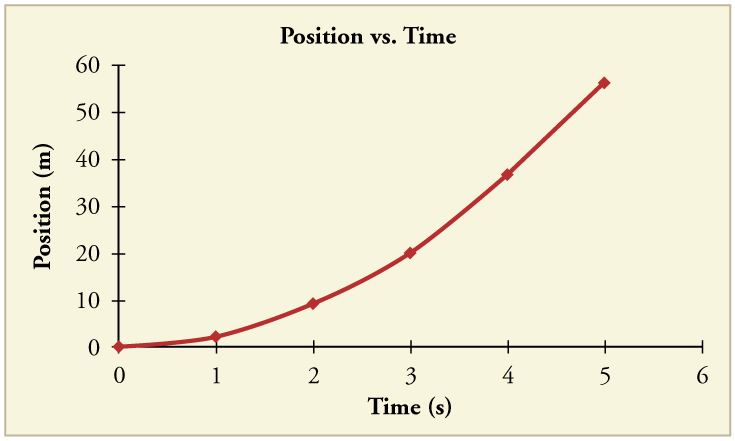
An Olympic-class sprinter starts a race with an acceleration of 4 . 50 m/s 2 size 12{4 "." "50 m/s" rSup { size 8{2} } } {} . (a) What is her speed 2.40 s later? (b) Sketch a graph of her position vs. time for this period.

(a) 10 . 8 m/s size 12{"10" "." 8" m/s"} {}

(b)

Line graph of position in meters versus time in seconds. The line begins at the origin and is concave up, with its slope increasing over time.

A well-thrown ball is caught in a well-padded mitt. If the deceleration of the ball is 2 . 10 × 10 4 m/s 2 , and 1.85 ms ( 1 ms = 10 − 3 s ) size 12{ \( "1 ms"="10" rSup { size 8{-3} } " s" \) } {} elapses from the time the ball first touches the mitt until it stops, what was the initial velocity of the ball?

38.9 m/s (about 87 miles per hour)

A bullet in a gun is accelerated from the firing chamber to the end of the barrel at an average rate of 6 .20 × 10 5 m/s 2 size 12{6 "." "20"´"10" rSup { size 8{5} } " m/s" rSup { size 8{2} } } {} for 8 . 10 × 10 − 4 s . What is its muzzle velocity (that is, its final velocity)?

(a) A light-rail commuter train accelerates at a rate of 1 . 35 m/s 2 size 12{1 "." "35 m/s" rSup { size 8{2} } } {} . How long does it take to reach its top speed of 80.0 km/h, starting from rest? (b) The same train ordinarily decelerates at a rate of 1 . 65 m/s 2 size 12{1 "." "65 m/s" rSup { size 8{2} } } {} . How long does it take to come to a stop from its top speed? (c) In emergencies the train can decelerate more rapidly, coming to rest from 80.0 km/h in 8.30 s. What is its emergency deceleration in m/s 2 size 12{"m/s" rSup { size 8{2} } } {} ?

(a) 16 . 5 s size 12{`"16" "." "5 s"} {}

(b) 13 . 5 s size 12{"13" "." "5 s"} {}

(c) − 2 . 68 m/s 2 size 12{` - 2 "." "68 m/s" rSup { size 8{2} } } {}

While entering a freeway, a car accelerates from rest at a rate of 2 . 40 m/s 2 size 12{2 "." "40 m/s" rSup { size 8{2} } } {} for 12.0 s. (a) Draw a sketch of the situation. (b) List the knowns in this problem. (c) How far does the car travel in those 12.0 s? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, check your units, and discuss whether the answer is reasonable. (d) What is the car’s final velocity? Solve for this unknown in the same manner as in part (c), showing all steps explicitly.

At the end of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of 2 . 00 m/s 2 size 12{2 "." "00 m/s" rSup { size 8{2} } } {} . (a) How far does she travel in the next 5.00 s? (b) What is her final velocity? (c) Evaluate the result. Does it make sense?

(a) 20 . 0 m size 12{"20" "." "0 m"} {}

(b) − 1 . 00 m/s size 12{ - 1 "." "00"`"m/s"} {}

(c) This result does not really make sense. If the runner starts at 9.00 m/s and decelerates at 2 . 00 m/s 2 size 12{2 "." "00 m/s" rSup { size 8{2} } } {} , then she will have stopped after 4.50 s. If she continues to decelerate, she will be running backwards.

Professional Application:

Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart. (a) Make a sketch of the situation. (b) List the knowns in this problem. (c) How long does the acceleration take? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units. (d) Is the answer reasonable when compared with the time for a heartbeat?
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Une: physics for the health professions. OpenStax CNX. Aug 20, 2014 Download for free at http://legacy.cnx.org/content/col11697/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Une: physics for the health professions' conversation and receive update notifications?

Ask