28.3 Photon energies and the electromagnetic spectrum  (Page 2/15)

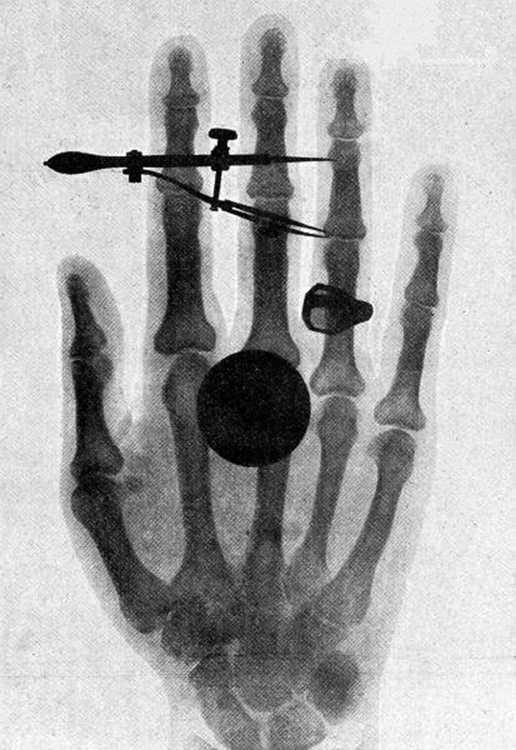
High photon energy also enables $\gamma$ rays to penetrate materials, since a collision with a single atom or molecule is unlikely to absorb all the $\gamma$ ray’s energy. This can make $\gamma$ rays useful as a probe, and they are sometimes used in medical imaging. x rays , as you can see in [link] , overlap with the low-frequency end of the $\gamma$ ray range. Since x rays have energies of keV and up, individual x-ray photons also can produce large amounts of ionization. At lower photon energies, x rays are not as penetrating as $\gamma$ rays and are slightly less hazardous. X rays are ideal for medical imaging, their most common use, and a fact that was recognized immediately upon their discovery in 1895 by the German physicist W. C. Roentgen (1845–1923). (See [link] .) Within one year of their discovery, x rays (for a time called Roentgen rays) were used for medical diagnostics. Roentgen received the 1901 Nobel Prize for the discovery of x rays.

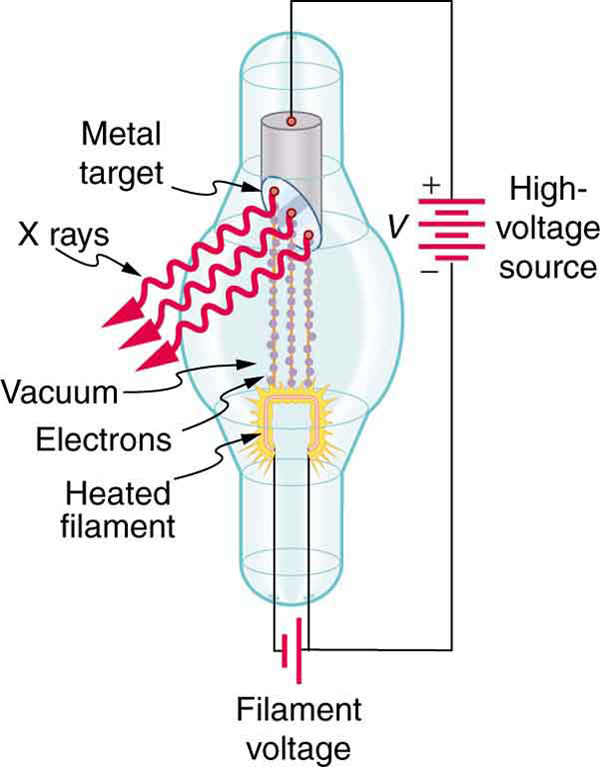
While $\gamma$ rays originate in nuclear decay, x rays are produced by the process shown in [link] . Electrons ejected by thermal agitation from a hot filament in a vacuum tube are accelerated through a high voltage, gaining kinetic energy from the electrical potential energy. When they strike the anode, the electrons convert their kinetic energy to a variety of forms, including thermal energy. But since an accelerated charge radiates EM waves, and since the electrons act individually, photons are also produced. Some of these x-ray photons obtain the kinetic energy of the electron. The accelerated electrons originate at the cathode, so such a tube is called a cathode ray tube (CRT), and various versions of them are found in older TV and computer screens as well as in x-ray machines.