21.7 Tunneling (Page 2/5)

Physics 101 Page 2 / 5

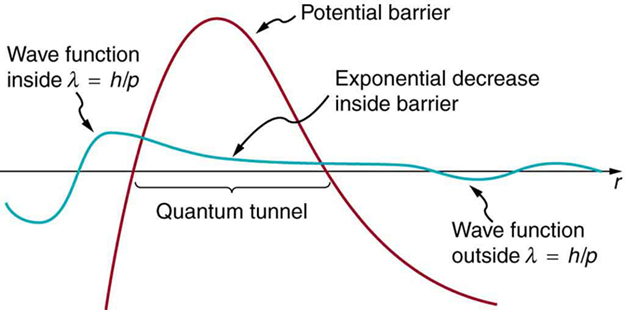
The image shows wave function curve and potential barrier quantum tunnel region. When the wave function curve passes through potential barrier it decreases exponentially. — The wave function representing a quantum mechanical particle must vary smoothly, going from within the nucleus (to the left of the barrier) to outside the nucleus (to the right of the barrier). Inside the barrier, the wave function does not abruptly become zero; rather, it decreases exponentially. Outside the barrier, the wave function is small but finite, and there it smoothly becomes sinusoidal. Owing to the fact that there is a small probability of finding the particle outside the barrier, the particle can tunnel through the barrier.

Good ideas explain more than one thing. In addition to qualitatively explaining how the four nucleons in an $α$ particle can get out of the nucleus, the detailed theory also explains quantitatively the half-life of various nuclei that undergo $α$ decay. This description is what Gamow and others devised, and it works for $α$ decay half-lives that vary by 17 orders of magnitude. Experiments have shown that the more energetic the $α$ decay of a particular nuclide is, the shorter is its half-life. Tunneling explains this in the following manner: For the decay to be more energetic, the nucleons must have more energy in the nucleus and should be able to ascend a little closer to the rim. The barrier is therefore not as thick for more energetic decay, and the exponential decrease of the wave function inside the barrier is not as great. Thus the probability of finding the particle outside the barrier is greater, and the half-life is shorter.

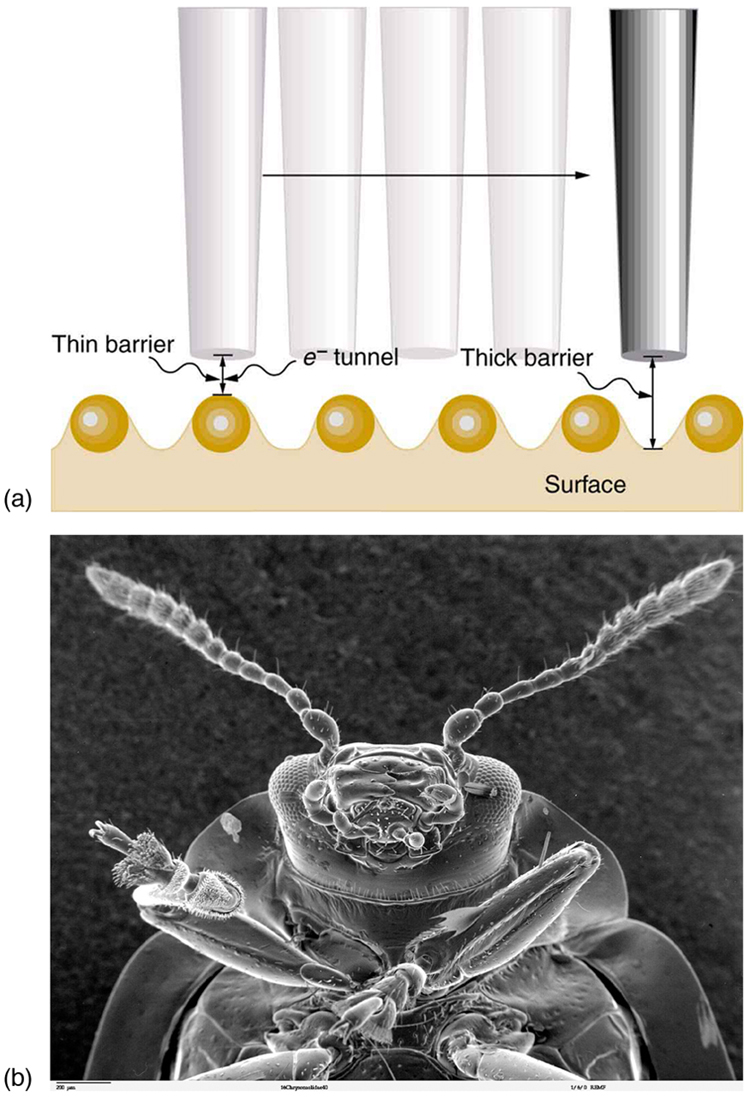
Tunneling as an effect also occurs in quantum mechanical systems other than nuclei. Electrons trapped in solids can tunnel from one object to another if the barrier between the objects is thin enough. The process is the same in principle as described for $α$ decay. It is far more likely for a thin barrier than a thick one. Scanning tunneling electron microscopes function on this principle. The current of electrons that travels between a probe and a sample tunnels through a barrier and is very sensitive to its thickness, allowing detection of individual atoms as shown in [link] .

Figure a shows a wavy surface with a taper cylindrical probe traveling horizontally toward right. Wherever there is a crest the barrier between probe and surface is thick and the barrier is thin when there is a hill on the surface. Figure b shows a scanning tunneling electron microscope image of an insect. — (a) A scanning tunneling electron microscope can detect extremely small variations in dimensions, such as individual atoms. Electrons tunnel quantum mechanically between the probe and the sample. The probability of tunneling is extremely sensitive to barrier thickness, so that the electron current is a sensitive indicator of surface features. (b) Head and mouthparts of *Coleoptera Chrysomelidea* as seen through an electron microscope (credit: Louisa Howard, Dartmouth College)

Phet explorations: quantum tunneling and wave packets

Watch quantum "particles" tunnel through barriers. Explore the properties of the wave functions that describe these particles.

Section summary

Tunneling is a quantum mechanical process of potential energy barrier penetration. The concept was first applied to explain $α$ decay, but tunneling is found to occur in other quantum mechanical systems.

Conceptual questions

A physics student caught breaking conservation laws is imprisoned. She leans against the cell wall hoping to tunnel out quantum mechanically. Explain why her chances are negligible. (This is so in any classical situation.)

When a nucleus $α$ decays, does the $α$ particle move continuously from inside the nucleus to outside? That is, does it travel each point along an imaginary line from inside to out? Explain.

Problems-exercises

Derive an approximate relationship between the energy of $α$ decay and half-life using the following data. It may be useful to graph the log of $t_{1/2}$ against $E_{α}$ to find some straight-line relationship.

Energy and half-life for $α$ Decay
Nuclide	$E_{α} (MeV)$	$t_{1/2}$
$^{216} Ra$	$9.5$	$0.18 μs$
$^{194} Po$	$7.0$	$0.7 s$
$^{240} Cm$	$6.4$	$27 d$
$^{226} Ra$	$4.91$	$1600 y$
$^{232} Th$	$4.1$	$1.4 \times 10^{10} y$

Integrated Concepts

A 2.00-T magnetic field is applied perpendicular to the path of charged particles in a bubble chamber. What is the radius of curvature of the path of a 10 MeV proton in this field? Neglect any slowing along its path.

22.8 cm

(a) Write the decay equation for the $α$ decay of $^{235} U$ . (b) What energy is released in this decay? The mass of the daughter nuclide is 231.036298 u. (c) Assuming the residual nucleus is formed in its ground state, how much energy goes to the $α$ particle?

(a) $_{92}^{235} U_{143} \to_{90}^{231} {Th}_{141} +_{2}^{4} {He}_{2}$

(b) 4.679 MeV

Unreasonable Results

The relatively scarce naturally occurring calcium isotope $^{48} Ca$ has a half-life of about $2 \times 10^{16} y$ . (a) A small sample of this isotope is labeled as having an activity of 1.0 Ci. What is the mass of the $^{48} Ca$ in the sample? (b) What is unreasonable about this result? (c) What assumption is responsible?

Unreasonable Results

A physicist scatters $γ$ rays from a substance and sees evidence of a nucleus $7.5 \times 10^{–13} m$ in radius. (a) Find the atomic mass of such a nucleus. (b) What is unreasonable about this result? (c) What is unreasonable about the assumption?

a) $2.4 \times 10^{8}$ u

(b) The greatest known atomic masses are about 260. This result found in (a) is extremely large.

Unreasonable Results

A frazzled theoretical physicist reckons that all conservation laws are obeyed in the decay of a proton into a neutron, positron, and neutrino (as in $β^{+}$ decay of a nucleus) and sends a paper to a journal to announce the reaction as a possible end of the universe due to the spontaneous decay of protons. (a) What energy is released in this decay? (b) What is unreasonable about this result? (c) What assumption is responsible?

(a) $–1.805 MeV$

(b) Negative energy implies energy input is necessary and the reaction cannot be spontaneous.

(c) Although all conversation laws are obeyed, energy must be supplied, so the assumption of spontaneous decay is incorrect.

Construct Your Own Problem

Consider the decay of radioactive substances in the Earth’s interior. The energy emitted is converted to thermal energy that reaches the earth’s surface and is radiated away into cold dark space. Construct a problem in which you estimate the activity in a cubic meter of earth rock? And then calculate the power generated. Calculate how much power must cross each square meter of the Earth’s surface if the power is dissipated at the same rate as it is generated. Among the things to consider are the activity per cubic meter, the energy per decay, and the size of the Earth.

<< Chapter < Page Page > Chapter >>

Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Physics 101. OpenStax CNX. Jan 07, 2013 Download for free at http://legacy.cnx.org/content/col11479/1.1

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Physics 101' conversation and receive update notifications?

Ask

	3 Psychology MCQ 2009 2 Exam By John Gabrieli Start Exam
	Psychology By OpenStax Read Online Course
	4 BOD Hemolymphatic -Dr. Han By Brooke Delaney Start Exam
	Chemistry By OpenStax Read Online Course
	Anthropology Biology Culture By Richley Crapo Start Assignment
	Journalism Midterm By Sheila Lopez Start Exam
	English Composition 2 Final Practice By Madison Christian Start Test
	Nutrition Exam By Hannah Sheth Start Quiz
©flickr: Eduardo	Nursing Education NU589 Program Outcomes By Karen Gowdey Start Quiz
	Anthropology Culture Personality By Richley Crapo Start Assignment