20.6 Relativistic energy  (Page 4/12)

Relativistically, we have $W_{\text{net}}={\text{KE}}_{\text{rel}}$ .

When motionless, we have $v=0$ and

so that ${\text{KE}}_{\text{rel}}=0$ at rest, as expected. But the expression for relativistic kinetic energy (such as total energy and rest energy) does not look much like the classical $\frac{1}{2}{\mathrm{mv}}^2$ . To show that the classical expression for kinetic energy is obtained at low velocities, we note that the binomial expansion for $\gamma$ at low velocities gives

A binomial expansion is a way of expressing an algebraic quantity as a sum of an infinite series of terms. In some cases, as in the limit of small velocity here, most terms are very small. Thus the expression derived for $\gamma$ here is not exact, but it is a very accurate approximation. Thus, at low velocities,

Entering this into the expression for relativistic kinetic energy gives

So, in fact, relativistic kinetic energy does become the same as classical kinetic energy when .

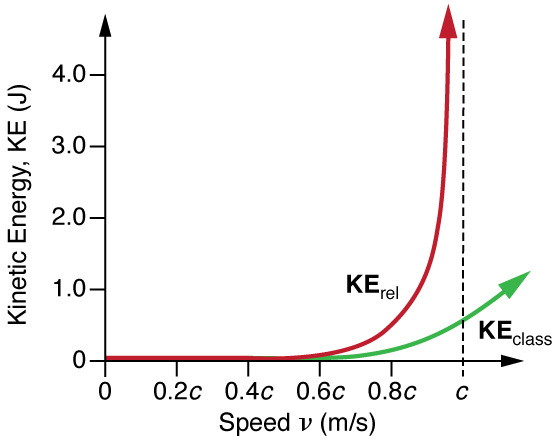
It is even more interesting to investigate what happens to kinetic energy when the velocity of an object approaches the speed of light. We know that $\gamma$ becomes infinite as $v$ approaches $c$ , so that KE _rel also becomes infinite as the velocity approaches the speed of light. (See [link] .) An infinite amount of work (and, hence, an infinite amount of energy input) is required to accelerate a mass to the speed of light.

So the speed of light is the ultimate speed limit for any particle having mass. All of this is consistent with the fact that velocities less than $c$ always add to less than $c$ . Both the relativistic form for kinetic energy and the ultimate speed limit being $c$ have been confirmed in detail in numerous experiments. No matter how much energy is put into accelerating a mass, its velocity can only approach—not reach—the speed of light.

Comparing kinetic energy: relativistic energy versus classical kinetic energy

An electron has a velocity $v=0\text{.}\text{990}c$ . (a) Calculate the kinetic energy in MeV of the electron. (b) Compare this with the classical value for kinetic energy at this velocity. (The mass of an electron is $9\text{.}\text{11}\times {\text{10}}^{-\text{31}}\text{kg}$ .)

Strategy

The expression for relativistic kinetic energy is always correct, but for (a) it must be used since the velocity is highly relativistic (close to $c$ ). First, we will calculate the relativistic factor $\gamma$ , and then use it to determine the relativistic kinetic energy. For (b), we will calculate the classical kinetic energy (which would be close to the relativistic value if $v$ were less than a few percent of $c$ ) and see that it is not the same.