2.9 Descriptive statistics: measuring the spread of the data  (Page 2/7)

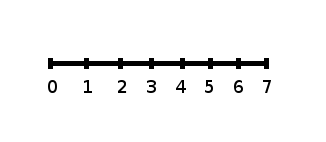
The number line may help you understand standard deviation. If we were to put 5 and 7 on a number line, 7 is to the right of 5. We say, then, that 7 is one standard deviation to the right of 5 because
$\mathrm{5\; +\; (1)(2)\; =\; 7}$ .

If 1 were also part of the data set, then 1 is two standard deviations to the left of 5 because
$\mathrm{5\; +\; (-2)(2)\; =\; 1}$ .

• In general, a value = mean + (#ofSTDEV)(standard deviation)
• where #ofSTDEVs = the number of standard deviations
• 7 is one standard deviation more than the mean of 5 because: 7=5+ (1) (2)
• 1 is two standard deviations less than the mean of 5 because: 1=5+ (−2) (2)

The equation value = mean + (#ofSTDEVs)(standard deviation) can be expressed for a sample and for a population:

• sample: $x=\overline{x}+\mathrm{(\#ofSTDEV)(s)}$
• Population: $x=\mu +\mathrm{(\#ofSTDEV)(\sigma )}$

Calculating the standard deviation

The procedure to calculate the standard deviation depends on whether the numbers are the entire population or are data from a sample. The calculations are similar, but not identical. Therefore the symbol used to represent the standard deviation depends on whether it is calculated from a population or a sample. The lower case letter $s$ represents the sample standard deviation and the Greek letter $\sigma$ (sigma, lower case) represents the population standard deviation. If the sample has the same characteristics as the population, then $s$ should be a good estimate of $\sigma$ .

To calculate the standard deviation, we need to calculate the variance first. The variance is an average of the squares of the deviations (the $x-$ $\overline{x}$ values for a sample, or the $x-\mu$ values for a population). The symbol ${\sigma }^2$ represents the population variance; the population standard deviation $\sigma$ is the square root of the population variance. The symbol $s^2$ represents the sample variance; the sample standard deviation $s$ is the square root of the sample variance. You can think of the standard deviation as a special average of the deviations.

If the numbers come from a census of the entire population and not a sample, when we calculate the average of the squared deviations to find the variance, we divide by N , the number of items in the population. If the data are from a sample rather than a population, when we calculate the average of the squared deviations, we divide by n-1 , one less than the number of items in the sample. You can see that in the formulas below.

Formulas for the sample standard deviation

• $s=$ $\sqrt{\frac{\Sigma {(x-\overline{x})}^2}{n-1}}$ or $s=$ $\sqrt{\frac{\Sigma {f·(x-\overline{x})}^2}{n-1}}$
• For the sample standard deviation, the denominator is n-1 , that is the sample size MINUS 1.

Formulas for the population standard deviation

• $\sigma =$ $\sqrt{\frac{\Sigma {(x-\overline{\mu })}^2}{N}}$ or $\sigma =$ $\sqrt{\frac{\Sigma {f·(x-\overline{\mu })}^2}{N}}$
• For the population standard deviation, the denominator is N , the number of items in the population.