| << Chapter < Page | Chapter >> Page > |
We have been exploring vectors and vector operations in three-dimensional space, and we have developed equations to describe lines, planes, and spheres. In this section, we use our knowledge of planes and spheres, which are examples of three-dimensional figures called surfaces , to explore a variety of other surfaces that can be graphed in a three-dimensional coordinate system.
The first surface we’ll examine is the cylinder. Although most people immediately think of a hollow pipe or a soda straw when they hear the word cylinder , here we use the broad mathematical meaning of the term. As we have seen, cylindrical surfaces don’t have to be circular. A rectangular heating duct is a cylinder, as is a rolled-up yoga mat, the cross-section of which is a spiral shape.
In the two-dimensional coordinate plane, the equation describes a circle centered at the origin with radius In three-dimensional space, this same equation represents a surface. Imagine copies of a circle stacked on top of each other centered on the z -axis ( [link] ), forming a hollow tube. We can then construct a cylinder from the set of lines parallel to the z -axis passing through circle in the xy -plane, as shown in the figure. In this way, any curve in one of the coordinate planes can be extended to become a surface.
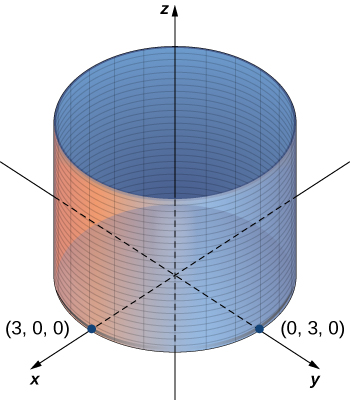
A set of lines parallel to a given line passing through a given curve is known as a cylindrical surface, or cylinder . The parallel lines are called rulings .
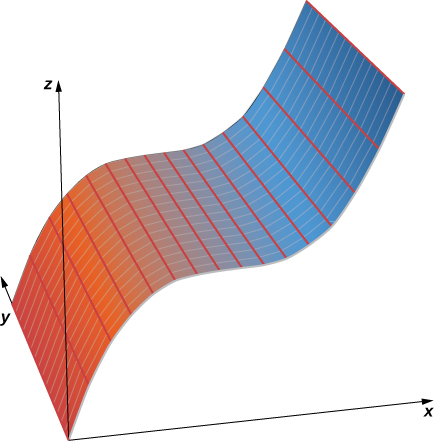
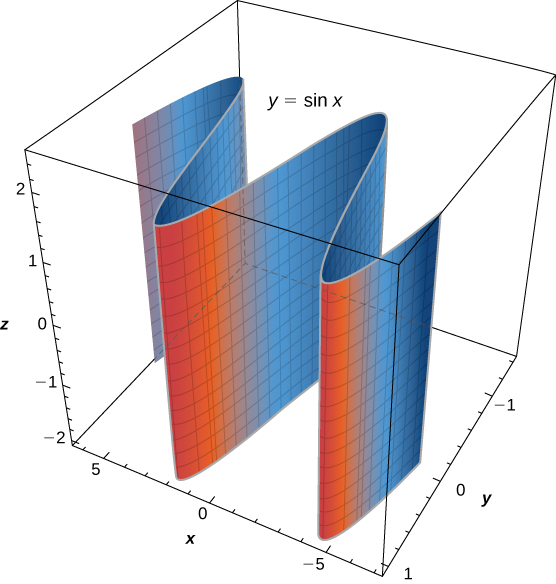
From this definition, we can see that we still have a cylinder in three-dimensional space, even if the curve is not a circle. Any curve can form a cylinder, and the rulings that compose the cylinder may be parallel to any given line ( [link] ).
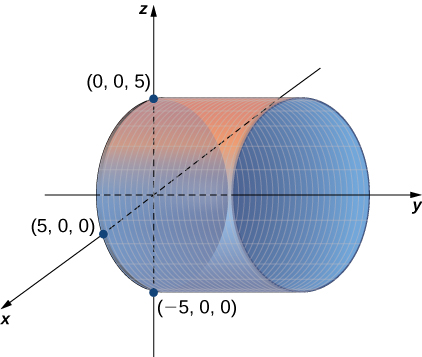
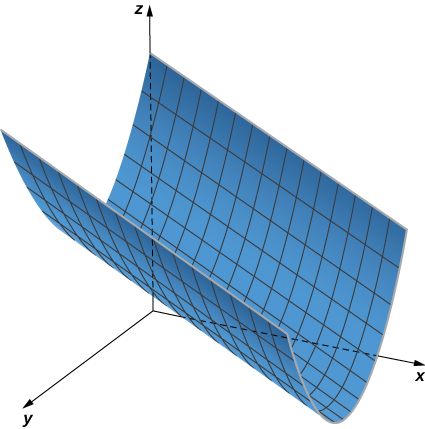
Sketch the graphs of the following cylindrical surfaces.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?