| << Chapter < Page | Chapter >> Page > |
This idea is not limited just to two point masses. In general, if n masses, are placed on a number line at points respectively, then the center of mass of the system is given by
Let be point masses placed on a number line at points respectively, and let denote the total mass of the system. Then, the moment of the system with respect to the origin is given by
and the center of mass of the system is given by
We apply this theorem in the following example.
Suppose four point masses are placed on a number line as follows:
Find the moment of the system with respect to the origin and find the center of mass of the system.
First, we need to calculate the moment of the system:
Now, to find the center of mass, we need the total mass of the system:
Then we have
The center of mass is located 1/2 m to the left of the origin.
Suppose four point masses are placed on a number line as follows:
Find the moment of the system with respect to the origin and find the center of mass of the system.
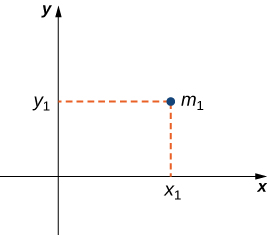
We can generalize this concept to find the center of mass of a system of point masses in a plane. Let be a point mass located at point in the plane. Then the moment of the mass with respect to the x -axis is given by Similarly, the moment with respect to the y -axis is given by Notice that the x -coordinate of the point is used to calculate the moment with respect to the y -axis, and vice versa. The reason is that the x -coordinate gives the distance from the point mass to the y -axis, and the y -coordinate gives the distance to the x -axis (see the following figure).
If we have several point masses in the xy -plane, we can use the moments with respect to the x - and y -axes to calculate the x - and y -coordinates of the center of mass of the system.
Let be point masses located in the xy -plane at points respectively, and let denote the total mass of the system. Then the moments and of the system with respect to the x - and y -axes, respectively, are given by
Also, the coordinates of the center of mass of the system are
The next example demonstrates how to apply this theorem.
Suppose three point masses are placed in the xy -plane as follows (assume coordinates are given in meters):
Find the center of mass of the system.
First we calculate the total mass of the system:
Next we find the moments with respect to the x - and y -axes:
Then we have
The center of mass of the system is in meters.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?