2.5 The onset of turbulence  (Page 29/3)

Sometimes we can predict if flow will be laminar or turbulent. We know that flow in a very smooth tube or around a smooth, streamlined object will be laminar at low velocity. We also know that at high velocity, even flow in a smooth tube or around a smooth object will experience turbulence. In between, it is more difficult to predict. In fact, at intermediate velocities, flow may oscillate back and forth indefinitely between laminar and turbulent.

An occlusion, or narrowing, of an artery, such as shown in [link] , is likely to cause turbulence because of the irregularity of the blockage, as well as the complexity of blood as a fluid. Turbulence in the circulatory system is noisy and can sometimes be detected with a stethoscope, such as when measuring diastolic pressure in the upper arm’s partially collapsed brachial artery. These turbulent sounds, at the onset of blood flow when the cuff pressure becomes sufficiently small, are called Korotkoff sounds . Aneurysms, or ballooning of arteries, create significant turbulence and can sometimes be detected with a stethoscope. Heart murmurs, consistent with their name, are sounds produced by turbulent flow around damaged and insufficiently closed heart valves. Ultrasound can also be used to detect turbulence as a medical indicator in a process analogous to Doppler-shift radar used to detect storms.

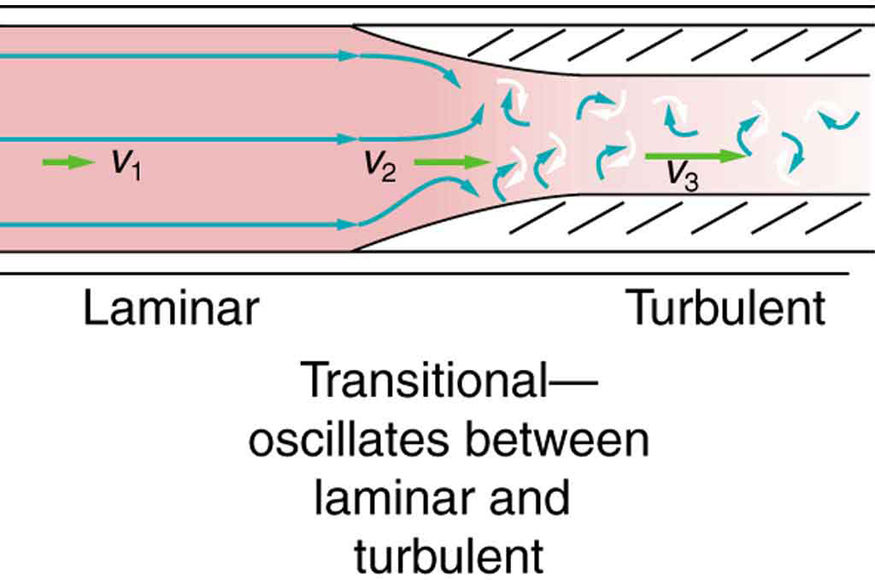
An indicator called the Reynolds number     $N_{\text{R}}$ can reveal whether flow is laminar or turbulent. For flow in a tube of uniform diameter, the Reynolds number is defined as

where $\rho$ is the fluid density, $v$ its speed, $\eta$ its viscosity, and $r$ the tube radius. The Reynolds number is a unitless quantity. Experiments have revealed that $N_{\text{R}}$ is related to the onset of turbulence. For $N_{\text{R}}$ below about 2000, flow is laminar. For $N_{\text{R}}$ above about 3000, flow is turbulent. For values of $N_{\text{R}}$ between about 2000 and 3000, flow is unstable—that is, it can be laminar, but small obstructions and surface roughness can make it turbulent, and it may oscillate randomly between being laminar and turbulent. The blood flow through most of the body is a quiet, laminar flow. The exception is in the aorta, where the speed of the blood flow rises above a critical value of 35 m/s and becomes turbulent.