This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses properties of multiplication of whole numbers. By the end of the module students should be able to understand and appreciate the commutative and associative properties of multiplication and understand why 1 is the multiplicative identity.
Section overview
- The Commutative Property of Multiplication
- The Associative Property of Multiplication
- The Multiplicative Identity
We will now examine three simple but very important properties of multiplication.
The commutative property of multiplication
Commutative property of multiplication
The product of two whole numbers is the same regardless of the order of the factors.
Sample set a
Multiply the two whole numbers.
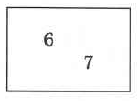
The numbers 6 and 7 can be multiplied in any order. Regardless of the order they are multiplied, the product is 42.
Got questions? Get instant answers now!
Practice set a
Use the commutative property of multiplication to find the products in two ways.
The associative property of multiplication
Associative property of multiplication
If three whole numbers are multiplied, the product will be the same if the first two are multiplied first and then that product is multiplied by the third, or if the second two are multiplied first and that product is multiplied by the first. Note that the order of the factors is maintained.
It is a common mathematical practice to
use parentheses to show which pair of numbers is to be combined first.
Sample set b
Multiply the whole numbers.
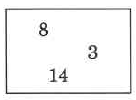
Got questions? Get instant answers now!
Practice set b
Use the associative property of multiplication to find the products in two ways.
The multiplicative identity
The multiplicative identity is 1
The whole number 1 is called the
multiplicative identity , since any whole number multiplied by 1 is not changed.
Sample set c
Practice set c
Multiply the whole numbers.
Exercises
For the following problems, multiply the numbers.
For the following 4 problems, show that the quantities yield the same products by performing the multiplications.
and
Got questions? Get instant answers now!
and
Got questions? Get instant answers now!
The fact that
is an example of the
property of multiplication.
Got questions? Get instant answers now!
The fact that
is an example of the
property of multiplication.
Got questions? Get instant answers now!
Exercises for review
(
[link] ) Replace the letter m with the whole number that makes the addition true.
Got questions? Get instant answers now!

