| << Chapter < Page | Chapter >> Page > |
Most students entering Algebra II are already familiar with the basic mechanics of graphing lines. Recapping very briefly: the equation for a line is where is the -intercept (the place where the line crosses the -axis) and m is the slope. If a linear equation is given in another form (for instance, ), the easiest way to graph it is to rewrite it in form (in this case, ).
There are two purposes of reintroducing this material in Algebra II. The first is to frame the discussion as linear functions modeling behavior . The second is to deepen your understanding of the important concept of slope.
Consider the following examples. Sam is a salesman—he earns a commission for each sale. Alice is a technical support representative—she earns $100 each day. The chart below shows their bank accounts over the week.
| After this many days (t) | Sam’s bank account (S) | Alice’s bank account (A) |
|---|---|---|
| 0 (*what they started with) | $75 | $750 |
| 1 | $275 | $850 |
| 2 | $375 | $950 |
| 3 | $450 | $1,050 |
| 4 | $480 | $1,150 |
| 5 | $530 | $1,250 |
Sam has some extremely good days (such as the first day, when he made $200) and some extremely bad days (such as the second day, when he made nothing). Alice makes exactly $100 every day.
Let d be the number of days, S be the number of dollars Sam has made, and A be the number of dollars Alice has made. Both S and A are functions of time. But is not a linear function , and is a linear function .
Once you know that Alice’s bank account function is linear, there are only two things you need to know before you can predict her bank account on any given day.
-intercept is relatively easy to understand. Verbally, it is where the function starts; graphically, it is where the line crosses the -axis.
But what about slope? One of the best ways to understand the idea of slope is to convince yourself that all of the following definitions of slope are actually the same.
| Definitions of Slope | ||
|---|---|---|
| In our example | In general | On a graph |
| Each day, Alice’s bank account increases by 100. So the slope is 100. | Each time the independent variable increases by 1, the dependent variable increases by the slope. | Each time you move to the right by 1, the graph goes up by the slope. |
| Between days 2 and 5, Alice earns $300 in 3 days. 300/3=100.Between days 1 and 3, she earns $200 in 2 days. 200/2=100. | Take any two points. The change in the dependent variable, divided by the change in the independent variable, is the slope. | Take any two points. The change in divided by the change in is the slope. This is often written as , or as |
| The higher the slope, the faster Alice is making moey. | The higher the slope, the faster the dependent variable increases. | The higher the slope, the faster the graph rises as you move to the right. |
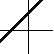
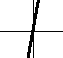
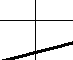
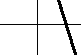
So slope does not tell you where a graph is, but how quickly it is rising. Looking at a graph, you can get an approximate feeling for its slope without any numbers. Examples are given below.


Notification Switch
Would you like to follow the 'Precalculus with engineering applications' conversation and receive update notifications?