1. Home
  2. College physics (engineering
  3. Fluid dynamics
  4. Viscosity and laminar flow;

2.4 Viscosity and laminar flow; poiseuille’s law  (Page 4/12)

<< Chapter < Page
  College physics (engineering     Page 4 / 12
Chapter >> Page >

The circulatory system provides many examples of Poiseuille’s law in action—with blood flow regulated by changes in vessel size and blood pressure. Blood vessels are not rigid but elastic. Adjustments to blood flow are primarily made by varying the size of the vessels, since the resistance is so sensitive to the radius. During vigorous exercise, blood vessels are selectively dilated to important muscles and organs and blood pressure increases. This creates both greater overall blood flow and increased flow to specific areas. Conversely, decreases in vessel radii, perhaps from plaques in the arteries, can greatly reduce blood flow. If a vessel’s radius is reduced by only 5% (to 0.95 of its original value), the flow rate is reduced to about ( 0 . 95 ) 4 = 0 . 81 size 12{ \( 0 "." "95" \) rSup { size 8{4} } =0 "." "81"} {} of its original value. A 19% decrease in flow is caused by a 5% decrease in radius. The body may compensate by increasing blood pressure by 19%, but this presents hazards to the heart and any vessel that has weakened walls. Another example comes from automobile engine oil. If you have a car with an oil pressure gauge, you may notice that oil pressure is high when the engine is cold. Motor oil has greater viscosity when cold than when warm, and so pressure must be greater to pump the same amount of cold oil.

The figure shows a section of a cylindrical tube of length l. The two end cross section are shown to have pressure P two and P one respectively. The radius of the cylindrical tube is given by r. The direction of flow is shown by horizontal arrows toward right end of the tube. The flow rate is marked as Q.
Poiseuille’s law applies to laminar flow of an incompressible fluid of viscosity η size 12{η} {} through a tube of length l size 12{l} {} and radius r size 12{r} {} . The direction of flow is from greater to lower pressure. Flow rate Q size 12{Q} {} is directly proportional to the pressure difference P 2 − P 1 size 12{P rSub { size 8{2} } - P rSub { size 8{1} } } {} , and inversely proportional to the length l size 12{l} {} of the tube and viscosity η size 12{η} {} of the fluid. Flow rate increases with r 4 size 12{r rSup { size 8{4} } } {} , the fourth power of the radius.

What pressure produces this flow rate?

An intravenous (IV) system is supplying saline solution to a patient at the rate of 0 . 120 cm 3 /s size 12{0 "." "120"``"cm" rSup { size 8{3} } "/s"} {} through a needle of radius 0.150 mm and length 2.50 cm. What pressure is needed at the entrance of the needle to cause this flow, assuming the viscosity of the saline solution to be the same as that of water? The gauge pressure of the blood in the patient’s vein is 8.00 mm Hg. (Assume that the temperature is 20ºC .)

Strategy

Assuming laminar flow, Poiseuille’s law applies. This is given by

Q = ( P 2 − P 1 ) π r 4 8 η l , size 12{Q= { { \( P rSub { size 8{2} } - P rSub { size 8{1} } \) π`r rSup { size 8{4} } } over {8ηl} } } {}

where P 2 size 12{P rSub { size 8{2} } } {} is the pressure at the entrance of the needle and P 1 size 12{P rSub { size 8{1} } } {} is the pressure in the vein. The only unknown is P 2 size 12{P rSub { size 8{2} } } {} .

Solution

Solving for P 2 size 12{P rSub { size 8{2} } } {} yields

P 2 = 8 η l πr 4 Q + P 1 . size 12{P rSub { size 8{2} } = { {8ηl} over {πr rSup { size 8{4} } } } Q+P rSub { size 8{1} } } {}

P 1 size 12{P rSub { size 8{1} } } {} is given as 8.00 mm Hg, which converts to 1 . 066 × 10 3 N/m 2 size 12{1 "." "066" times "10" rSup { size 8{3} } `"N/m" rSup { size 8{2} } } {} . Substituting this and the other known values yields

P 2 = 8 ( 1 . 00 × 10 − 3 N ⋅ s/m 2 ) ( 2 . 50 × 10 − 2 m ) π ( 0 . 150 × 10 − 3 m ) 4 ( 1 . 20 × 10 − 7 m 3 /s ) + 1 . 066 × 10 3 N/m 2 = 1 . 62 × 10 4 N/m 2 .

Discussion

This pressure could be supplied by an IV bottle with the surface of the saline solution 1.61 m above the entrance to the needle (this is left for you to solve in this chapter’s Problems and Exercises), assuming that there is negligible pressure drop in the tubing leading to the needle.

Flow and resistance as causes of pressure drops

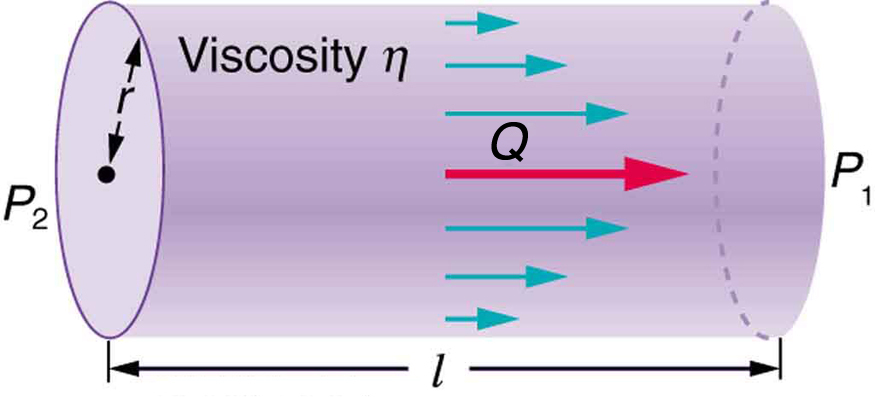
You may have noticed that water pressure in your home might be lower than normal on hot summer days when there is more use. This pressure drop occurs in the water main before it reaches your home. Let us consider flow through the water main as illustrated in [link] . We can understand why the pressure P 1 size 12{P rSub { size 8{1} } } {} to the home drops during times of heavy use by rearranging
<< Chapter < Page Page > Chapter >>
Practice Key Terms 5

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics (engineering physics 2, tuas). OpenStax CNX. May 08, 2014 Download for free at http://legacy.cnx.org/content/col11649/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics (engineering physics 2, tuas)' conversation and receive update notifications?

Ask