2.4 Electric field: concept of a field revisited  (Page 28/5)

Contact forces, such as between a baseball and a bat, are explained on the small scale by the interaction of the charges in atoms and molecules in close proximity. They interact through forces that include the Coulomb force    . Action at a distance is a force between objects that are not close enough for their atoms to “touch.” That is, they are separated by more than a few atomic diameters.

For example, a charged rubber comb attracts neutral bits of paper from a distance via the Coulomb force. It is very useful to think of an object being surrounded in space by a force field . The force field carries the force to another object (called a test object) some distance away.

Concept of a field

A field is a way of conceptualizing and mapping the force that surrounds any object and acts on another object at a distance without apparent physical connection. For example, the gravitational field surrounding the earth (and all other masses) represents the gravitational force that would be experienced if another mass were placed at a given point within the field.

In the same way, the Coulomb force field surrounding any charge extends throughout space. Using Coulomb’s law, $F=k\mathrm{|}{q}_1{q}_2\mathrm{|}/r^2$ , its magnitude is given by the equation $F=k\mathrm{|}\mathrm{qQ}\mathrm{|}/r^2$ , for a point charge    (a particle having a charge $Q$ ) acting on a test charge     $q$ at a distance $r$ (see [link] ). Both the magnitude and direction of the Coulomb force field depend on $Q$ and the test charge $q$ .

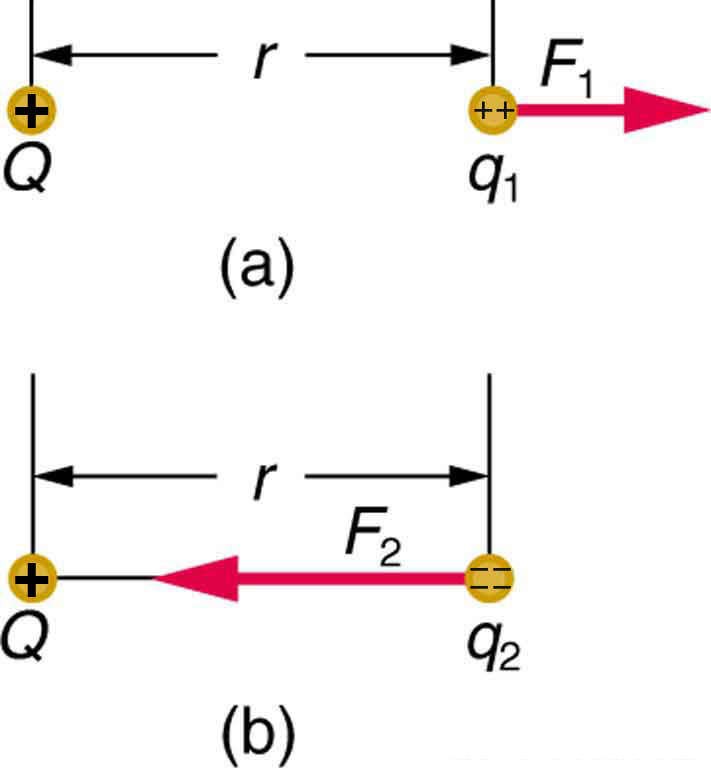
To simplify things, we would prefer to have a field that depends only on $Q$ and not on the test charge $q$ . The electric field is defined in such a manner that it represents only the charge creating it and is unique at every point in space. Specifically, the electric field $E$ is defined to be the ratio of the Coulomb force to the test charge:

where $\mathbf{\text{F}}$ is the electrostatic force (or Coulomb force) exerted on a positive test charge $q$ . It is understood that $\mathbf{\text{E}}$ is in the same direction as $\mathbf{\text{F}}$ . It is also assumed that $q$ is so small that it does not alter the charge distribution creating the electric field. The units of electric field are newtons per coulomb (N/C). If the electric field is known, then the electrostatic force on any charge $q$ is simply obtained by multiplying charge times electric field, or $\mathbf{\text{F}}=q\mathbf{\text{E}}$ . Consider the electric field due to a point charge $Q$ . According to Coulomb’s law, the force it exerts on a test charge $q$ is $F=k\mathrm{|}\mathrm{qQ}\mathrm{|}/r^2$ . Thus the magnitude of the electric field, $E$ , for a point charge is