2.3 Vector addition and subtraction: analytical methods  (Page 33/6)

Learning objectives

By the end of this section, you will be able to:

• Understand the rules of vector addition and subtraction using analytical methods.
• Apply analytical methods to determine vertical and horizontal component vectors.
• Apply analytical methods to determine the magnitude and direction of a resultant vector.

The information presented in this section supports the following AP® learning objectives and science practices:

• 3.A.1.1 The student is able to express the motion of an object using narrative, mathematical, and graphical representations. (S.P. 1.5, 2.1, 2.2)

Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.

Resolving a vector into perpendicular components

Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like $\mathbf{A}$ in [link] , we may wish to find which two perpendicular vectors, ${\mathbf{A}}_x$ and ${\mathbf{A}}_y$ , add to produce it.

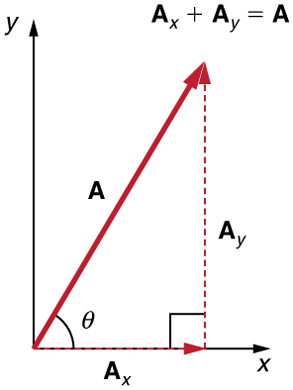
${\mathbf{A}}_x$ and ${\mathbf{A}}_y$ are defined to be the components of $\mathbf{A}$ along the x - and y -axes. The three vectors $\mathbf{A}$ , ${\mathbf{A}}_x$ , and ${\mathbf{A}}_y$ form a right triangle:

Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if ${\mathbf{\text{A}}}_x=\mathrm{3\; m}$ east, ${\mathbf{\text{A}}}_y=\mathrm{4\; m}$ north, and $\mathbf{\text{A}}=\mathrm{5\; m}$ north-east, then it is true that the vectors ${\mathbf{A}}_x{\text{ + A}}_y\text{ = A}$ . However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,

Thus,

If the vector $\mathbf{A}$ is known, then its magnitude $A$ (its length) and its angle $\theta$ (its direction) are known. To find $A_x$ and $A_y$ , its x - and y -components, we use the following relationships for a right triangle.

and

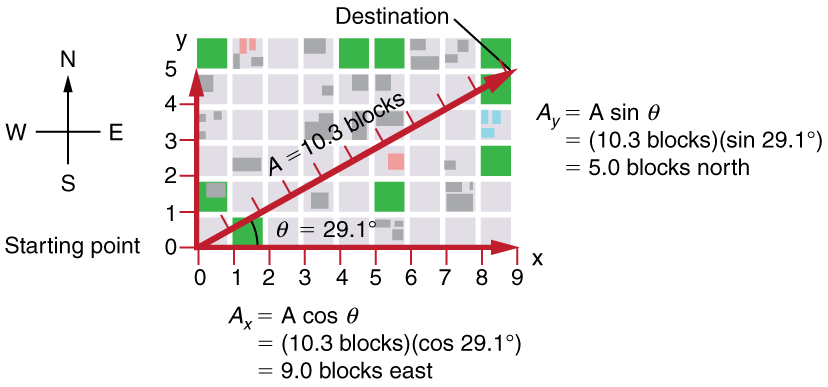
Suppose, for example, that $\mathbf{A}$ is the vector representing the total displacement of the person walking in a city considered in Kinematics in Two Dimensions: An Introduction and Vector Addition and Subtraction: Graphical Methods .