| << Chapter < Page | Chapter >> Page > |
Gasoline consumption in the United States has been steadily increasing. Consumption data from 1994 to 2004 is shown in [link] . http://www.bts.gov/publications/national_transportation_statistics/2005/html/table_04_10.html Determine whether the trend is linear, and if so, find a model for the data. Use the model to predict the consumption in 2008.
| Year | '94 | '95 | '96 | '97 | '98 | '99 | '00 | '01 | '02 | '03 | '04 |
| Consumption (billions of gallons) | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
The scatter plot of the data, including the least squares regression line, is shown in [link] .
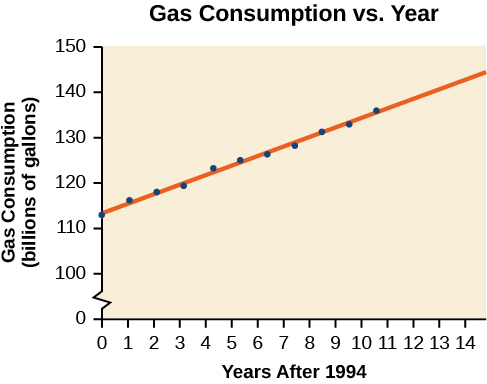
We can introduce new input variable, representing years since 1994.
The least squares regression equation is:
Using technology, the correlation coefficient was calculated to be 0.9965, suggesting a very strong increasing linear trend.
Using this to predict consumption in 2008
The model predicts 144.244 billion gallons of gasoline consumption in 2008.
Use the model we created using technology in [link] to predict the gas consumption in 2011. Is this an interpolation or an extrapolation?
150.871 billion gallons; extrapolation
Access these online resources for additional instruction and practice with fitting linear models to data.
Describe what it means if there is a model breakdown when using a linear model.
When our model no longer applies, after some value in the domain, the model itself doesn’t hold.
What is interpolation when using a linear model?
What is extrapolation when using a linear model?
We predict a value outside the domain and range of the data.
Explain the difference between a positive and a negative correlation coefficient.
Explain how to interpret the absolute value of a correlation coefficient.
The closer the number is to 1, the less scattered the data, the closer the number is to 0, the more scattered the data.
A regression was run to determine whether there is a relationship between hours of TV watched per day and number of sit-ups a person can do The results of the regression are given below. Use this to predict the number of sit-ups a person who watches 11 hours of TV can do.

Notification Switch
Would you like to follow the 'Selected topics in algebra' conversation and receive update notifications?